Internal resistance seen by the voltage source, Vx?

In summary, the conversation discusses an op-amp configuration and how to calculate the resistance seen through the voltage source. The answer is 3kΩ but the individual is unsure how to find it. They also clarify that the title should have stated resistance instead of internal resistance. Additionally, they label the current in the top 1k resistor as Ix and ask for assistance in marking the magnitude and direction of the current in the other 4 input resistors.
  • #1
Kratos321
20
0
Hi everyone,

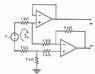
I have attached an image of the op-amp configuration (all op-amps are ideal). Basically, the question asks to calculate the resistance seen through the voltage source. The answer is 3 kΩ but I just don't understand how this is found. If someone could assist me, I would really appreciate it.

(By the way, I mean just resistance in the title, not internal resistance)

Cheers
 

Attachments

  • internal_resistance.JPG
    internal_resistance.JPG
    18.3 KB · Views: 434
Last edited:
Physics news on Phys.org
  • #2
You have labelled the current flowing in that top 1k resistor as Ix. Using the notation you have established, now mark in the magnitude and direction of the current in each of the other 4 input resistors.
 

FAQ: Internal resistance seen by the voltage source, Vx?

1. What is internal resistance in a voltage source?

Internal resistance is the resistance that is present within a voltage source, such as a battery or power supply. It is caused by the materials and structure of the source itself and can affect the flow of current through the circuit.

2. How does internal resistance affect the output voltage of a source?

Internal resistance can cause a decrease in the output voltage of a source, especially when the current drawn from the source is high. This is because the internal resistance creates a voltage drop within the source, reducing the overall output voltage.

3. Can internal resistance be eliminated?

No, internal resistance cannot be completely eliminated. However, it can be minimized by using high-quality materials and design in the construction of the voltage source. Additionally, using a larger source with lower internal resistance can also help reduce its impact.

4. How does internal resistance affect the power output of a source?

Internal resistance can cause a decrease in the power output of a source, as some of the energy is lost within the source itself. This is why it is important to choose a source with low internal resistance, especially for high-power applications.

5. Can internal resistance change over time?

Yes, internal resistance can change over time due to factors such as aging, temperature, and usage. This is why it is important to regularly test and maintain voltage sources to ensure their performance is not significantly affected by changes in internal resistance.

Similar threads

Internal Resistance Affect the Balancing Length in a Potentiometer?
Replies
12
Views
413
Connecting a number of EMF sources in a circle to form a circuit
Replies
9
Views
462
Parallel circuit with internal resistance
Replies
6
Views
1K
How to solve for EMF and internal resistance in a circuit?
Replies
8
Views
2K
Finding the internal resistance of battery
Replies
10
Views
3K
Input Resistance of this BJT Amplifier
Replies
12
Views
2K
Incandescent Bulb - suitable approximation for voltage-current curve
Replies
2
Views
437
Unraveling the Mystery of EMF Internal Resistance
Replies
2
Views
2K
Find the voltage across the resistor
Replies
3
Views
1K
The voltage across an AC source and a resistance in series
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top