ClapClap
- 24
- 0
I have performed an impact test on different football shin guards to assess their performance. I am however confused with the readings measured by the accelerometer I have used. The sensor was attached to a striking mass of 4.3 kg which was dropped at different heights.
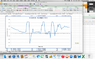
The graph I have attached shows the data collected by the accelerometer (y-axis) versus the time (x-axis) for an impact test at drop height of 20 cm.
Can anyone help me understand how to read this data? (i assume the graph looks messy because they weight 'bounced off' the shin guard a few times).
How can I use this data to assess guards performance?
The graph I have attached shows the data collected by the accelerometer (y-axis) versus the time (x-axis) for an impact test at drop height of 20 cm.
Can anyone help me understand how to read this data? (i assume the graph looks messy because they weight 'bounced off' the shin guard a few times).
How can I use this data to assess guards performance?