Interpretation of electronic bands in a solid

In summary, the conversation discusses questions about the E(k) diagram and its corresponding bands. The speaker is seeking to understand the basics of the diagram and how it relates to different materials. They also mention the concept of Γ and its role in the diagram. They make statements about the Fermi level and how it relates to the number of filled bands at different temperatures. Finally, they mention the possibility of the diagram corresponding to the semimetals Ge or As.
  • #1
Keru
20
1

Homework Statement


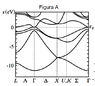
The exercise asks many questions about the following E(k) diagram, but I'm more interested in understanding some basic things about it, from which I'm sure i'll be able to find the answers I'm requested.

bands.png

1) What do the bands actually correspond to? Is the lowest band corresponding to 1s2 molecular orbital, the upper to 2s2 2p6 and so on?
2) I have several diagrams and all of them contain a "Γ", what is the meaning of that 'k' apparently common to every band diagram?
3) Looking at the Fermi level, would this statements be true?
3.1) At 0K the first 4 bands would be full, and the rest empty.
3.2) At a little higher temperature (let's say 0,1eV more for the Fermi level), the first three bands would be full, while the next two partially filled.
4) If 1) was correct, by looking at the intersection of Fermi level and Γ, the graphic could only correspond to the semimetals Ge or As, right?

Thanks in advantage for any help.
 

Attachments

  • bands.png
    bands.png
    24.1 KB · Views: 361
Physics news on Phys.org
  • #2
This site has some good explanations. Basically, the Γ corresponds to a specific symmetry direction in k-space. One comment on your point 4) - Ge is a semiconductor, not a semimetal.

EDIT - I meant to say a particular symmetry direction.
 
Last edited:

1. What is the electronic band structure of a solid and why is it important?

The electronic band structure of a solid refers to the distribution of energy levels that electrons can occupy within the solid. It is important because it determines the electrical and optical properties of the material, such as its conductivity and color.

2. How is the electronic band structure of a solid determined?

The electronic band structure of a solid can be determined through experimental techniques such as photoemission spectroscopy or theoretical calculations such as density functional theory.

3. What is the difference between a conductor, insulator, and semiconductor in terms of electronic bands?

Conductors have partially filled or overlapping bands that allow electrons to move freely, making them good conductors of electricity. Insulators have completely filled bands and large band gaps, making it difficult for electrons to move and thus are poor conductors. Semiconductors have partially filled bands with small band gaps, allowing for some movement of electrons and making them intermediate conductors.

4. How does the band structure change with temperature and pressure?

At higher temperatures, electrons have more thermal energy and can jump to higher energy levels, causing the bands to broaden. At higher pressures, the spacing between atoms decreases, causing the energy levels to shift closer together.

5. How does the band structure affect the properties of different materials?

The band structure of a material determines its electrical, optical, and magnetic properties. For example, materials with a narrow band gap are often used in solar cells, while those with a wide band gap are used in LEDs. Materials with partially filled bands are good conductors, while those with completely filled bands are insulators.

Similar threads

Band theory: effective mass and Hall's coefficient
    • Advanced Physics Homework Help
Replies
2
Views
1K
Solid State Physics: Draw the Dispersion Relation from the Fermi Surface
    • Advanced Physics Homework Help
Replies
1
Views
2K
I How does diffusion of high energy electrons shift band structure?
    • Atomic and Condensed Matter
Replies
1
Views
1K
Nearly free electron model: band gap
    • Advanced Physics Homework Help
Replies
1
Views
1K
A Electronic band structure of iron superconductor BaFe2As2
    • Atomic and Condensed Matter
Replies
4
Views
2K
Doping with gallium and arsenic
    • Advanced Physics Homework Help
Replies
3
Views
2K
Fermi Energy Matching in Semiconductors
    • Advanced Physics Homework Help
Replies
1
Views
4K
Semiconductor Sub-band Occupancy
    • Advanced Physics Homework Help
Replies
1
Views
2K
A Thermal Properties of the Free Electron Gas: Fermi-Dirac Distribution
    • Atomic and Condensed Matter
Replies
1
Views
2K
Band Structure of a solid is not related to the size/doping?
    • Atomic and Condensed Matter
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top