Inverse Laplace transform of a rational function

[room_]

TL;DR

I struggle to find an appropriate inverse Laplace transform of the following
$$ 2^n a^n \frac{p^{n-1}}{(p+a)^{2n}}, \quad a>0$$

I struggle to find an appropriate inverse Laplace transform of the following
$$F(p)= 2^n a^n \frac{p^{n-1}}{(p+a)^{2n}}, \quad a>0.$$
WolframAlpha gives as an answer
$$f(t)= 2^n a^n t^n \frac{_1F_1 (2n;n+1;-at)}{\Gamma(n+1)}, \quad (_1F_1 - \text{confluent hypergeometric function})$$
which seem to work for my original problem, but only for small $n$ (<50). Whenever I go close or above 50 (I use Matlab to plot things) the outcome gets bizarre ($n=50$):

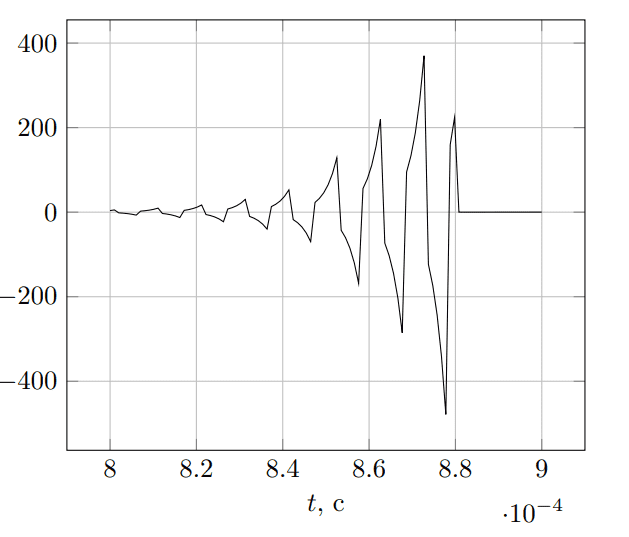although the actual simulation result (the process which is described by $F(p)$) looks as it meant to be, smoothly getting to the shape on the following figure ($n=49$).

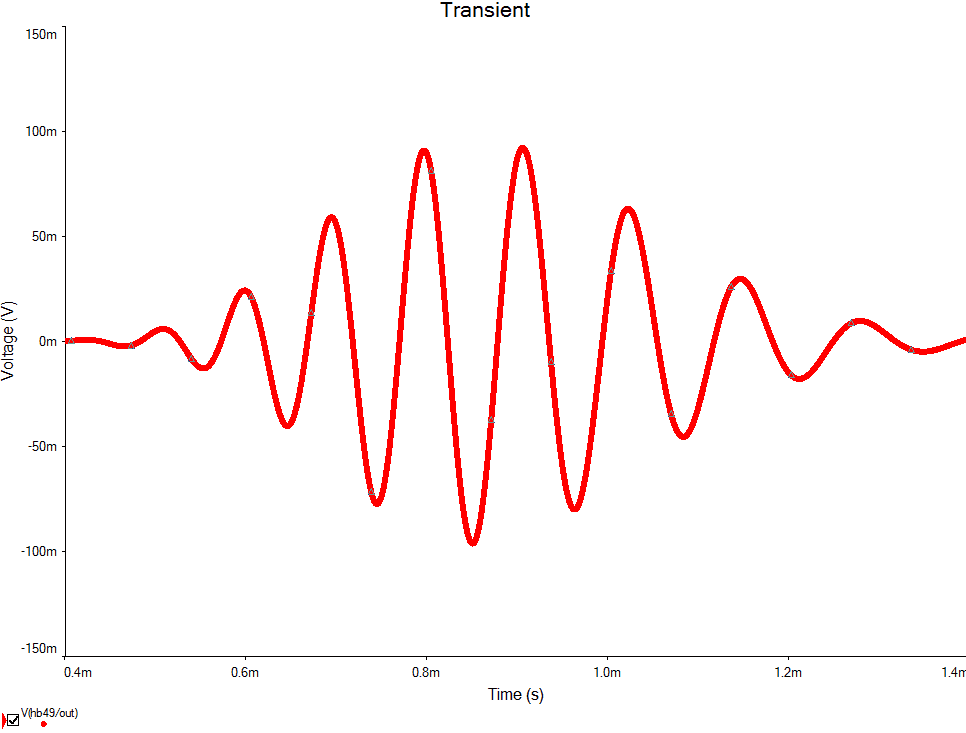Therefore I conclude there is something wrong with the $f(t)$ given out by Wolfram. Using the Laplace transform handbook (russian one, idk if it's reasonable to link) the best I could do was$$\hat{F}(p)= 2^n a^n \frac{p^{n}}{(p+a)^{2n}} \div \frac{2^n a^n}{\Gamma(2n)}\frac{d^{n-1}}{dt^{n-1}}(e^{-at}t^{2n-1})=\hat{f}(t), $$
since (as the handbook suggests)
$$ \left( \frac{p}{p+1} \right)^{n+1}\frac{1}{(p+1)^a}\div \frac{n!}{\Gamma(n+a+1)}e^{-t}t^a L_n^a(t), \ L_n^a(t)=\frac{e^tt^{-a}}{n!}\frac{d^n}{dt^n} (e^{-t}t^{n+a}),$$
which I'm not sure is legitimate to use (because of $n+1$ power), yet it yields somewhat fine solution for my original problem (which is strange, because obviously $F(p)\ne \hat{F}(p)$). I tried to plot it, and for small $n$ it is fine, but Matlab refuses to calculate the derivative (it spits out 0) for $n>30$, so I cannot check whether it really suits. So my question is whether the Wolfram answer is wrong. I'm not really familiar with the confluent hypergeometric function, so I don't know how to interpret the outcome. What would you suggest to calculate the $F(p)$? Is it even possible to do in elementary functions? I'd appreciate any help in the solution. I am aware of possibility that my reasoning is wrong, so in case of that let me know. Thank you for help!

 

[benorin]

Well, this will not answer all your queries: but it’ll give you somewhere to start.

From the definition of $_1F_1$ here (with p=q=1) $$f(t)= 2^n a^n t^n \frac{_1F_1 (2n;n+1;-at)}{\Gamma(n+1)} = \tfrac{2^n a^n t^n}{\Gamma(n+1)}\sum_{k=0}^{\infty}(-1)^k \tfrac{\left( 2n\right) _{k}}{\left( n+1\right) _{k}k!}a^k t^k$$

where $(a)_{k}:= \tfrac{\Gamma (a+k)}{\Gamma (a)}$ is a pochhammer symbol (there are some otherwise defined for different domains and a simplification on that page).

I encourage you to write out that $\tfrac{d^{n-1}}{dt^{n-1}}(\cdots )$ product rule as the binomial-like identity in terms of the sum of powers of differential operators (on this page) for the inverse Laplace transform you had and see if it’s not equivalent to- or a truncated form of- the wolfram confluent hypergeometric Function above. GL.

 

[room_]

Thank you for your response.

I encourage you to write out that $\tfrac{d^{n-1}}{dt^{n-1}}(\cdots )$ product rule as the binomial-like identity in terms of the sum of powers of differential operators

I had and idea to write it out using exponential shift theorem, so here is my reasoning
$$
\frac{d^{n-1}}{dt^{n-1}} (e^{-\omega_c t}t^{2n-1}) = D^{n-1}(e^{-\omega_c t}t^{2n-1})=
e^{-\omega_c t}(D-\omega_c)^{n-1} t^{2n-1} = \\
= e^{-\omega_c t}\sum_{k=0}^{n-1}(-1)^{n-1-k}\omega_c^{n-1-k}C_{n-1}^{k}D^{k}t^{2n-1} = \\
= e^{-\omega_c t}\sum_{k=0}^{n-1}(-1)^{n-1-k}\omega_c^{n-1-k}C_{n-1}^{k} (2n-1)\ldots (2n-k)t^{2n-1-k},
$$
where $C_{n-1}^{k}$ are binomial coefficients. Doesn't seem equivalent to $_1F_1$.