Inverted Pendulum on Cart: What is this term in the KE?

[jstluise]

I am working through an example of an inverted pendulum on a cart, exactly like this:

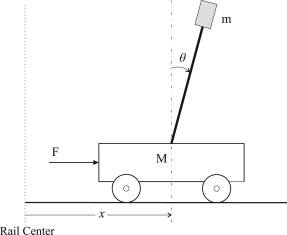
L is the length of the massless pendulum arm.

Two degrees of freedom, x and theta. If I write out the kinetic energy as three parts: translational KE from cart + translational KE from pendulum + rotational KE from pendulum, I end up missing a term (compared to writing out the KE in vector form with each mass).

In vector form:

T = \frac{1}{2}M\dot{r_{1}}\cdot\dot{r_{1}} + \frac{1}{2}m\dot{r_{2}}\cdot\dot{r_{2}}
T = \frac{1}{2}M\dot{x}^{2} + \frac{1}{2}m(\dot{x}^{2}+{l^2}{\dot{\theta}^2}+2l\dot{x}\dot{\theta}cos{\theta})

I know above is correct, but I don't know what the term ml\dot{x}\dot{\theta}cos{\theta} represents.

If I write the KE using the other method, I get

T = \frac{1}{2}M\dot{x}^{2} + \frac{1}{2}m\dot{x}^{2}+\frac{1}{2}m{l^2}{\dot{\theta}^2}

where each term represents translational KE from cart, translational KE from pendulum, and rotational KE from pendulum, respectively. I am missing the term from the KE that was obtained using vectors.

I think I'm missing the velocity component of the pendulum mass in the y direction?

 

[AlephZero]

The horizontal component of the velocity of $m$ is $\dot x + l \cos\theta\, \dot \theta$
And the vertical component (downwards) is is $l \sin\theta\, \dot \theta$.

So the resultant velocity squared is $(\dot x + l \cos\theta\, \dot \theta)^2 + (l \sin\theta\, \dot \theta)^2$

The last expression for $T$ is wromg, because it is the KE of the cart measured relative to the ground, plus the KE of the pendulum measured relative to the cart. You can't work in two different coordinate frames at the same time.

 

[jstluise]

The horizontal component of the velocity of $m$ is $\dot x + l \cos\theta\, \dot \theta$
And the vertical component (downwards) is is $l \sin\theta\, \dot \theta$.

So the resultant velocity squared is $(\dot x + l \cos\theta\, \dot \theta)^2 + (l \sin\theta\, \dot \theta)^2$

The last expression for $T$ is wromg, because it is the KE of the cart measured relative to the ground, plus the KE of the pendulum measured relative to the cart. You can't work in two different coordinate frames at the same time.

Thanks, makes sense.

So is there any equation that is used for finding $T$ of a rigid body that is rotating about a arbitrary, moving axis? For example, pretend the inverted pendulum is not a point mass on the end of a massless rod, but rather a rod of mass $m$ and length $l$. The axis of rotation of the rod is at the cart, and the center of mass in in the center of the bar.

If the axis of rotation was fixed, I could use the parallel axis theorem and find $T$ due to the rotation only. But, since the axis is moving, I have translational energy, too.

I think the long and short of it is that when working with any translation and rotating rigid body, it is best to only work its center of mass. And only in the special case of having a fixed axis can you use the parallel axis theorem. Does that sound correct?

 

[AlephZero]

If you are using some generalized coordinates to describe the motion of the complete system, then you can use them to describe the translation and rotation of the CM of some part of the system.

So there isn't really any need to use the parallel axis theorem, etc.

IMO the best way to learn these topics is to learn to be methodical. Eventually you will start to recognize combinations of variables that you have seen before and just "write down the answer", but taking short cuts doesn't save time if you get lost along the way.

 

[road_king]

The horizontal component of the velocity of $m$ is $\dot x + l \cos\theta\, \dot \theta$
And the vertical component (downwards) is is $l \sin\theta\, \dot \theta$.

So the resultant velocity squared is $(\dot x + l \cos\theta\, \dot \theta)^2 + (l \sin\theta\, \dot \theta)^2$

The last expression for $T$ is wrong, because it is the KE of the cart measured relative to the ground, plus the KE of the pendulum measured relative to the cart. You can't work in two different coordinate frames at the same time.

That does not make sense to me. The KE of the pendulum is measured relative to the ground because $\dot x + l \cos\theta\, \dot \theta$ ... $\dot x$ express movement relative to the ground. (Plus the rotation relative to the cart).. Please shed some light..