david90
- 311
- 2
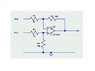
please look at this circuit
http://hyperphysics.phy-astr.gsu.edu/Hbase/Electronic/ietron/inva2.gif
The transfer function for the the circuit above is
Vout = (-Rf/Rs)*Vs
if I were to switch the terminal of the op amp so that Vin is inputted into Vp and Vn =0 instead (everything is the same except that Op amp terminal Vp is now Vn and Vn and is now Vp), how does it change the behavior of the circuit? The transfer function is still the same but I doubt the behavior of the circuit is the same. Or is it?
http://hyperphysics.phy-astr.gsu.edu/Hbase/Electronic/ietron/inva2.gif
The transfer function for the the circuit above is
Vout = (-Rf/Rs)*Vs
if I were to switch the terminal of the op amp so that Vin is inputted into Vp and Vn =0 instead (everything is the same except that Op amp terminal Vp is now Vn and Vn and is now Vp), how does it change the behavior of the circuit? The transfer function is still the same but I doubt the behavior of the circuit is the same. Or is it?