palaphys
- 235
- 12
- Homework Statement
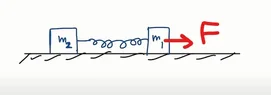
- Two bars of masses m1 and m2 connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?
- Relevant Equations
- WET, F=kx
The diagram above describes the situation. Say the spring constant is k. The main goal will be to apply the condition that when the spring force exactly balances the limiting friction, m2 will begin to slide. i.e ##kx=μm_2g##
I came up with two approaches for this one.
i) Assume that m1 is in equilibrium, so balance the spring force and frictional force with the external force.
ii)Apply WET between the two points, initial position and the final position, i.e where the velocity of m1 becomes zero.
method i) yields a solution for F which is less than ii), but the result from ii) is given as the right position. Not able to comprehend why.
Help is appreciated. Thanks.
Attachments
Last edited by a moderator: