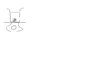unscientific
- 1,728
- 13
What is the reading on the scale for the first one?? My friend mentioned that upthrust need not be considered as its an 'internal force', i wonder why??
Shouldnt' the net force dowards be (Weight of stone - pVg) + (Weight of water + pVg) as the water experiences an equal an opposite downthrust (exerted by the stone on water) due to it exerting upthrust on stone?
For the 2nd case there is a string,
the net force downwards be (Weight of stone - pVg - T) + (Weight of water + pVg), as the water experiences an equal an opposite downthrust (exerted by the stone on water) due to it exerting upthrust on stone?
Furthermore, since the ball is in static and dynamic equilibrium, T + pVg = mg, therefore (Weight of stone - pVg - T) = 0
So the reading no the scale would be = Weight of water + pVg(further workings)
The difference in scale readings would be (Weight of water + weight of iron ball) - (Weight of water + pVg) = Weight of iron ball - pVg = T
So the difference is just tension T.
Shouldnt' the net force dowards be (Weight of stone - pVg) + (Weight of water + pVg) as the water experiences an equal an opposite downthrust (exerted by the stone on water) due to it exerting upthrust on stone?
For the 2nd case there is a string,
the net force downwards be (Weight of stone - pVg - T) + (Weight of water + pVg), as the water experiences an equal an opposite downthrust (exerted by the stone on water) due to it exerting upthrust on stone?
Furthermore, since the ball is in static and dynamic equilibrium, T + pVg = mg, therefore (Weight of stone - pVg - T) = 0
So the reading no the scale would be = Weight of water + pVg(further workings)
The difference in scale readings would be (Weight of water + weight of iron ball) - (Weight of water + pVg) = Weight of iron ball - pVg = T
So the difference is just tension T.
Attachments
Last edited: