Is Force Truly a Scalar in Rope Friction Problems?

[Happiness]

Consider a rope wraps an angle $\theta$ around a pole with a coefficient of static friction $\mu$. You pull one end with a tension $T_0$. The force that the other end can support is given by $T=T_0e^{\mu\theta}$(derivation below). For $\mu=1$ and $\theta=2\pi$, $T=530T_0$. That means with the help of static friction, you can wrap a rope one round around a pole to hold up a weight 530 times $T_0$! Suppose I can carry a maximum weight of 50 kg tied to a rope. By wrapping the rope once around a pole, I'll be able to support $530\times50=26500$kg! That's the weight of an aeroplane! Doesn't this sound dubious? But this is what is claimed by the book below.

Next, let's explain why force is a scalar here. The reason why the tension at the other end is $530T_0$ is because static friction is always acting in the same direction along the rope, say anticlockwise. This static friction at different parts of the rope is being summed up as a scalar to give a value of $529T_0$. Then add this to the $T_0$ you exert, we get $T=530T_0$.

If we treat friction as a vector instead, we will say that the friction at different parts of the rope is in different directions. When the rope is wrapped once, the vector sum of friction is zero since vectors arranged in a circle go back to the same point.

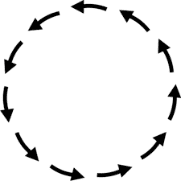
Then, we will conclude $T=T_0$. After wrapping the rope once around a pole, the maximum weight I can support remains the same.

Which is correct? The scalar sum or the vector sum?

 

[Orodruin]

It is not forces that are being considered, it is the string tension. Depending on how you make across section of the string, you will get different directions. What matters is getting an expression for the tension as a function of the angle and this is what is done.

Of course, a constant of friction of one is huge and the result depends exponentially on $\mu$.

 

[Happiness]

It is not forces that are being considered, it is the string tension. Depending on how you make across section of the string, you will get different directions. What matters is getting an expression for the tension as a function of the angle and this is what is done.

Of course, a constant of friction of one is huge and the result depends exponentially on $\mu$.

Could you explain why the vector-sum model is wrong? That is, why isn't the vector sum of friction zero?

If the friction are the vectors shown below, then shouldn't they add up to zero?

 

[Orodruin]

Could you explain why the vector-sum model is wrong? That is, why isn't the vector sum of friction zero?

If the friction are the vectors shown below, then shouldn't they add up to zero?
View attachment 103277

The friction is not constant around the loop.

 

[Happiness]

Of course, a constant of friction of one is huge and the result depends exponentially on $\mu$.

But even with a constant of friction of $0.1$, I only need to wrap the rope around the pole ten times to lift an aeroplane. That's still very incredible!

 

[Orodruin]

The rope or the pole will break before you can lift an aeroplane.
"Needless to say, the limiting factor in such a case is not your strength, but the structural integrity of the pole around which the rope winds."

 

[Orodruin]

Of course, there is also a reason you find constructions such as these on sailing boats:

 

[Chestermiller]

The analysis involves performing a local differential force balance on a tiny section of the rope (not the entire wrap of rope), and applying force equilibrium to the tiny section of rope in the local directions normal and tangent to the pole. This is similar to what we do when we consider a particle motion in which forces are acting normal and tangent to the particle trajectory. In the case of the rope, the local normal force per unit length of rope (from the force balance in the normal direction) is n=T/R. In the tangential direction, the force balance gives:

$$T(\theta + d\theta)-T(\theta)=\mu (nR\Delta \theta)$$

If we divide this equation by $\Delta \theta$ and take the limit as $\Delta \theta$ approaches zero, we obtain:
$$\frac{dT}{d\theta}=\mu nR=\mu T$$

 

[Happiness]

The friction is not constant around the loop.

The derivation starts with $dT=\mu N$, which means the change in tension is equal to the friction on the little piece of rope. Then integration is performed on both sides. That means the total change in tension is equal to the scalar sum of all the friction on the little pieces. But why is it a scalar sum? For example, $W=\int\mathbf{F}\cdot d\mathbf{s}$ is a scalar sum.

Since the friction is not constant, the vector sum of all the friction is not zero. But because some of the friction partially cancels out, the vector sum should be less than the scalar sum. But why is this not taken into account?

EDIT: I've found the reason. I think it's because the LHS $\int dT$ is also a scalar sum.

 

[Orodruin]

Since the friction is not constant, the vector sum of all the friction is not zero. But because some of the friction partially cancels out, the vector sum should be less than the scalar sum. But why is this not taken into account?

You are looking at the tension in the rope, not the total force sum on the rope or pole. These are different concepts.

 

[CWatters]

Of course, there is also a reason you find constructions such as these on sailing boats:

Indeed. If anyone ever asks you to help tie up a boat and throws you a rope never just stand there holding it - way too easy to get pulled in. Always put a turn around a suitable post or ring etc. You don't have to tie it, just put a turn around and hold the end. I'm not at all surprised you gain a factor or 500 advantage.

 

[Orodruin]

Always put a turn around a suitable post or ring etc.

And by "suitable" we mean a post that will be able to hold the boat without breaking ...

 

[anorlunda]

Indeed. If anyone ever asks you to help tie up a boat and throws you a rope never just stand there holding it - way too easy to get pulled in. Always put a turn around a suitable post or ring etc. You don't have to tie it, just put a turn around and hold the end. I'm not at all surprised you gain a factor or 500 advantage.

Actually, the magic number is three turns. See http://dickandlibby.blogspot.com/2014/02/the-magic-number-three.html
One is too little. More than three (as shown in the picture in post #7) are prone to fouling. Three turns will let you hold any force up to the strength of the line using only slight force on the tailing end.

 

[wrobel]

Actually these are forces and vectors. Perhaps the authors of the text that is cited in OP should be little bit precise and formal. This problem can easily be generalized. Assume that the pole is a convex oval in its horizontal section (shaded area in the picture) :

The ends of the rope are pulled with forces $\boldsymbol G$ and $\boldsymbol F$. Then the system remains in equilibrium provided
$$ e^{-\mu\alpha}\le \frac{|\boldsymbol F|}{|\boldsymbol G|}\le e^{\mu\alpha},$$ here $\alpha$ is an angle from the vector $-\boldsymbol F$ to the vector $\boldsymbol G$ (clockwise ).
To prove this theorem it is convenient to expand the equations of equilibrium for the small arc of the rope by the Frenet frame