Is the Quadrangle in the Geometry Challenge a Square?

[henrique_p]

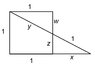
Well, I found this challenge in another forum (not about math) on the internet, and, originally, there were no 'w', 'z' or 'y' drawn on the pic, it was just "find the x", but I put them on because I know you guys probably would create other variables to solve the problem.
Another problem I had to deal with is if the Quadrangle is, by fact, a square, I mean, if 'w' plus 'z' really is 1. How the wreck do I solve this?

 

[mathman]

(y/1) = (1+y)/(1+x) (both are secants of the same angle)

1 + (1+x)² = (1+y)² (Pthag. theorem)

I'll let you do the algebra.

 

[acabus]

(y/1) = (1+y)/(1+x) (both are secants of the same angle)

1 + (1+x)² = (1+y)² (Pthag. theorem)

I'll let you do the algebra.

Could you do (y/1) = (1/x) instead?

 

[henrique_p]

Could you do (y/1) = (1/x) instead?

Yes, in this case x=y$^{-1}$.

 

[henrique_p]

(y/1) = (1+y)/(1+x) (both are secants of the same angle)

Just another doubt, how can I know if the biggest triangle (1, 1+x, 1+y) has a 90º base angle? Because it wasn't specified in the problem if there is a square.

 

[mathman]

Just another doubt, how can I know if the biggest triangle (1, 1+x, 1+y) has a 90º base angle? Because it wasn't specified in the problem if there is a square.

It is still OK even if is not a square. If it is a rhombus, the triangles involved are similar, so the side ratios {y:1 = (1+y):(1+x)} are equal, even if not the secant of the angle.

If it is not a rhombus, then I suspect there is no solution.

 

[mathman]

Added note: In case of a rhombus, you need to know the angle, so that you can use the law of cosines to get the secon equation.

 

[henrique_p]

Ok, by doing the algebra I found the equation on the pic. I don't know if this was right, so I went to Wolfram to solve this.

 

[willem2]

Ok, by doing the algebra I found the equation on the pic. I don't know if this was right, so I went to Wolfram to solve this.

No real solutions, so it wasn't right.

combining

a) w+z = 1
b) x^2 + z ^2 = 1
c) w^2 + 1 = y^2
d) y/1 = 1/x

use c amd d to get

e) w^2 + 1 = 1/x^2

and then a and e to get

f) z^2 - 2z +2 = 1/x^2

and finally b and f to get

g) (z^2 - 2z+2)(1-z^2) = 1

feeding this to wolfram alpha:

http://www.wolframalpha.com/input/?i=%28z^2+-+2z+%2B2%29%281+-+z^2%29+%3D+1%2C+sqrt%281-+z^2%29

gets you x ≈ 0.883204

 

[mathman]

Ok, by doing the algebra I found the equation on the pic. I don't know if this was right, so I went to Wolfram to solve this.

Your original equation looks wrong.

I got: y⁴ + 2y³ - y² -2y -1 = 0.

A quick inspection shows there is a root between 1 and √2, which is expected.

 

[henrique_p]

Your original equation looks wrong.

I got: y⁴ + 2y³ - y² -2y -1 = 0.

A quick inspection shows there is a root between 1 and √2, which is expected.

Am I wrong or I can divide this equation by (y-1)?

 

[mathman]

Am I wrong or I can divide this equation by (y-1)?

1 is not a root, so you can't divide by y-1.

 

[henrique_p]

1 is not a root, so you can't divide by y-1.

Yeah, sure, I miscounted the coefficients.