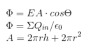You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Is There Flux Through the Lateral Surface of a Cylinder?
AI Thread Summary
The discussion centers on whether there is flux through the lateral surface of a cylinder. Participants clarify that the relevant area for calculating flux is the surface area of the ends of the Gaussian surface, which is πR². The equation for electric flux, Φ = EA = Q enclosed / ε, is confirmed, with a specific example calculating Q enclosed as 27.8 pC. It is emphasized that the lateral area formula (A = 2πrh) does not apply in this context, as there is no flux through the lateral surface. Ultimately, the conclusion is that there is no flux through the lateral surface of the cylinder in this problem.
Physics news on Phys.org
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Your expressions for the areas don't look correct. When calculating ##\Phi_0##, what particular area are you working with? What is the formula for this particular area ?
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Which parts of the surface of the cylinder have nonzero flux?
Fatima Hasan
- 315
- 14
The area that we're concerned will be the surface area of the ends of Gaussian surface which is equals to π / R^2TSny said:Which parts of the surface of the cylinder have nonzero flux?
Φ = E A = Q enclosed / ε
Q enclosed = ## 100 * π * (0.1)^2 * 8.85 = 27.8 pC ##
Last edited:
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
Of course you mean π⋅R^2.Fatima Hasan said:The area that we're concerned will be the surface area of the ends of Gaussian surface which is equals to π / R^2
This is correct.Φ = E A = Q enclosed / ε
Q enclosed = 100 * π * (0.1)^2 * 8.85 = 27.8 pC
Fatima Hasan
- 315
- 14
##A = 2 \pi r h## , we use this formula to find the net flux through a cylinder , right ?TSny said:Of course you mean π⋅R^2.
This is correct.
Last edited:
TSny
Science Advisor
Homework Helper
Gold Member
- 14,761
- 4,773
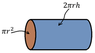
Not in this problem. The area ##A = 2 \pi r h## is the "lateral" area of the curved surface of the cylinder, as shown below in blueFatima Hasan said:##A = 2 \pi r h## , we use this formula to find the net flux through a cylinder , right ?
Is there any flux through the blue surface in the problem you are working on?
Attachments
Fatima Hasan
- 315
- 14
NoTSny said:Not in this problem. The area ##A = 2 \pi r h## is the "lateral" area of the curved surface of the cylinder, as shown below in blue
View attachment 221399
Is there any flux through the blue surface in the problem you are working on?
Similar threads
- Replies
- 7
- Views
- 2K
- Replies
- 26
- Views
- 1K
- Replies
- 16
- Views
- 967
- Replies
- 9
- Views
- 491
- Replies
- 4
- Views
- 694
- Replies
- 7
- Views
- 3K
- Replies
- 14
- Views
- 850
- Replies
- 1
- Views
- 3K
- Replies
- 10
- Views
- 10K
- Replies
- 2
- Views
- 2K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math