Is this answer incorrect for cancelling waves?

[Perseverence]

Homework Statement

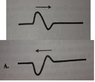
A wave is traveling to the right shown in the first picture. Which wave traveling to the left will momentarily cancel out the original wave moving to the right?

Homework Equations

There are no equations, this problem is visual

The Attempt at a Solution

It seems the answer C, in picture two, is the correct answer because the small dip in the original wave would first encounter the small upward bump coming from the right side. And then the large upward bump in the original wave coming from the left would then encounter the large dip and wait C cancelling them out. Wave A as the answer seems to have the original wave with a small dip encountering a large dip coming from the wave on the right first. This seems like it would not create a cancellation, but rather a larger dip combining the two dips together. I'm totally confused. The answer seems so straightforward that it would be answers C, but it is wrong

 

[kuruman]

t seems the answer C, in picture two, is the correct answer because the small dip in the original wave would first encounter the small upward bump coming from the right side. And then the large upward bump in the original wave coming from the left would then encounter the large dip and wait C cancelling them out.

Cancelling the peaks is not enough. The waves must cancel everywhere. Compare the part of the waves between the small and large peaks. They are sloping in the same direction matching positive with positive above the baseline and negative with negative below the baseline. Can they cancel if that's the case?

 

[Perseverence]

I see what you are saying about the peaks, but how can they cancel without the peak amplitudes being equal as they encounter each other?

 

[kuruman]

I see what you are saying about the peaks, but how can they cancel without the peak amplitudes being equal as they encounter each other?

Sorry, I was comparing the wrong waveform. It looks to me that (C) is the correct answer. You say that's not the case. Why? Do you know what is supposed to be the correct answer?

 

[Perseverence]

The solution set says " The answer is A. The two waves, if superposed ,would add to zero at every point"

Perhaps the solution is wrong. That is a load off my mind to see that someone else agrees with me, because the confusion was maddening.

I could only see "A" as the answer, if the waves were moving in the same direction.

 

[kuruman]

Also A and D cancel if they move in opposite directions. That's what I looked at earlier forgetting that A is not the given wave.

 

[mjc123]

The answer is A because, as they pass each other, there will be a moment when the displacement of A is equal and opposite to that of the original wave at all points simultaneously, i.e. A will be the reflection of original in a horizontal plane. This is not true for C - the small peaks will cancel out as they meet, then the large peaks (not exactly as they are unsymmetrical), but not both simultaneously. The same is true of A and D.

 

[tnich]

Cancelling the peaks is not enough. The waves must cancel everywhere. Compare the part of the waves between the small and large peaks. They are sloping in the same direction matching positive with positive above the baseline and negative with negative below the baseline. Can they cancel if that's the case?

kuruman, I think you were correct here. At some moment in time, the two waves must cancel everywhere. That means that one must be a reflection of the other in the horizontal axis. So A is the correct choice.
C is not the correct choice. It would cancel each point in the wave at some time, but not all points simultaneously.

 

[Perseverence]

but they approach each other from opposide sides. A only seems like it would be the answer if they started superposed, moving in the SAME direction

 

[tnich]

but they approach each other from opposide sides. A only seems like it would be the answer if they started superposed, moving in the SAME direction

If they started out superposed and moved in the same direction, then they would cancel at all times.
You seem to be saying that if they start superposed, they would cancel at that moment.

 

[CWatters]

Draw them one above the other then add them vertically ..

 

[Perseverence]

If they started out superposed and moved in the same direction, then they would cancel at all times.
You seem to be saying that if they start superposed, they would cancel at that moment.

moved in the same direction, then they would cancel at all times.
You seem to be saying that if they start superposed, they would cancel at that moment.[/QUOTE]


Right. But they DO NOT start out superposed. That's why there are directional arrows. The first thing that would meet would be the small dip in the given wave and athe Large dip in wave A which would create a third even larger dip. If it doesn't matter in which order ih the elements of the two different waves meet, then I don't know what the point is of the directional arrows.

 

[kuruman]

Ah, yes of course. The cancellation is expected to be momentary according to the question. I was trying to get the waveform to cancel at all times while the waves overlap.

 

[Merlin3189]

I wonder if people are being mislead by the word 'cancel'?
The waves do not cancel each other, IMO even momentarily. Both waves continue to exist during and after their encounter.

At one instant as they pass, the sum of whatever is represented by the vertical axis - maybe displacement, if they are waves on a rope - is zero everywhere. But that does not mean there is not some other property of the waves - maybe the velocity of the rope in that case - which is not zero everywhere at that instant.

The momentary interference to give zero for the vertical axis that we are looking for here is satisfied only when the waves are mirror images and traveling in opposite directions. If they were traveling in the same direction at the same speed, then either they would not be coincident, in which case they would never cancel nor interfere, or they would be coincident, in which case IMO neither would ever exist nor ever have existed!
What it might mean to have two waves of identical shape traveling in the same medium in the same direction at different speeds, I can't say.

 

[kuruman]

What it might mean to have two waves of identical shape traveling in the same medium in the same direction at different speeds, I can't say.

If the waves are mirror-images traveling in the same direction at different speeds, then the faster moving waveform will catch up with the slower moving waveform and there will be momentary superposition of zero amplitude. If the fast moving waveform is ahead of the other one, then as long as the slow waveform was generated first, then there must have been a moment of zero amplitude some time in the past. It's the relative velocity that counts. In the example posted by OP, you can assume that the given waveform is frozen in time while the answer waveform comes by at any speed towards it and the answer will be the same. If you are OK with this, then consider the situation in which you, the observer, are moving to the right with speed that is greater than the speed of the waveform moving to the left. You will see both wave forms moving to the right at different speeds and adding to zero amplitude at the same position on the medium as when you are at rest relative to the medium.

 

[Perseverence]

Merlin, Kuruman, Do you think the answer is C or A?

At the very least, I'm glad to see this question is not as straightforward as maybe it should be.

 

[CWatters]

I can't see anything in the question that might make B,C or D correct.

 

[CWatters]

Two waves going in the same direction at different speeds is a different question but to cancel they would still need to be mirror images of each other in the vertical plane so A with the arrow reversed is the nearest.

 

[Perseverence]

Ok, so what I've learned from this is that no matter what direction the waves are travelling, to cancel their amplitudes, they need to be mirror images of each other, correct?

 

[Merlin3189]

To Perseverance: A.

To everyone else: Yes I should have said a wave and its inverse traveling in the same direction.

To everyone, esp Kuruman: The point about waves traveling in the same direction at different speeds was that I could not think how this would be possible. I can see waves of different frequencies having different speeds in the same medium, but not two matching wave packets. Even if one wave packet is the inverse of the other, its spectral composition should be the same. Only the phases have been changed.

 

[kuruman]

To everyone, esp Kuruman: The point about waves traveling in the same direction at different speeds was that I could not think how this would be possible. I can see waves of different frequencies having different speeds in the same medium, but not two matching wave packets. Even if one wave packet is the inverse of the other, its spectral composition should be the same. Only the phases have been changed.

I see what you're saying. I concentrated more on what the waves would look like and less on the feasibility of generating identical waves traveling at different speeds.