Joao said:
What other explanation could there be, other than a random event in the future determined if the photon behaved as a particle or wave in the first detector? [...] It seems so clear that the traditional order of cause and effects wasn't followed
It only seems clear because explanations of the DCQE are basically terrible on purpose. They explain things backwards, and then confuse the explanation being backwards with causality being backwards.
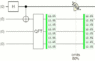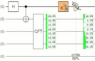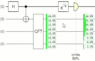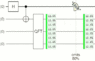
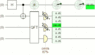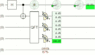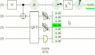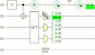
Here's what happens when I simulate the DCQE with my quantum circuit simulator Quirk:
In the above circuit, the top line is akin to the idler photon and the next three lines are akin to the screen-hitting photon. The green box in the middle is showing how often the screen photon hits various parts of the screen, before we condition on the idler photon. Notice that it's evenly spread out (there's no wavy interference pattern). This matches what is recorded in the experiments.
Now we measure the idler photon
and focus on just the runs where that measurement result occurs. In other words, we look at our data and throw out the 50% of runs where the opposite idler measurement occurred and look at where the screen photon landed
in the remaining half of runs we kept. This is why the diagram has a dashed lined from the detector to a note of "omits 50%". (This is where typical terrible articles start talking about "backwards in time effects", as if you throwing out half of your data corresponded to rewriting history instead of just... looking at a specific half of it.)
If we measure the idler without rotating it first, i.e. we measure it along the Z axis, this doesn't do anything interesting. Both possible remaining halves are also evenly spread out. But if we measure it along the Y axis (by rotating it 90 degrees around the X axis before measuring along Z), then the two possible remaining halves do differ from each other. They make complementary wavy-looking patterns. (The total original data is still flat without waves.)
---
The green expectation displays I'm showing in the diagram can be a bit misleading, because in a real experiment you don't get direct access to the expectations. You have to reconstruct them after the fact. So it's a bit helpful to reverse the situation and also consider how the
screen landing position affects the
idler.
If we focus on the experimental runs where a particular screen landing position occurs, and figure out the corresponding state of the idler, this is what we get:
Now the tall green rectangle is showing the screen landing position. Notice that the green box in the top right, which is showing how likely the idler measurement is to return ON instead of OFF, stays rock-solid at 50% when the X^1/2 gate is not present but flips out when the gate is present. But the green sphere things are
always flipping out.
The green spheres are showing the idler's state as a vector on the Bloch sphere. The important point is that a) the screen landing position affects which way that vector points (due to entanglement) but b) it's always pointing along the XY plane, and c) Z-axis measurements only depend on how up-or-down the vector points. If we measure along Z, all that crazy conditional spinning in the XY plane has no effect on the on-vs-off probability. But if we measure along X or along Y (or rotate before measuring along Z), then the crazy conditional spinning
does affect our expectations.
So instead of telling a backwards-in-time story about the idler photon measurement causing the screen position, we can tell a forwards-in-time story about the screen position determining the idler photon's state and thereby affecting its measurement. We simply choose whether to measure in a way that shows this effect, or in a way that is independent of it.
Though... really we shouldn't be telling
either the forward-in-time or backward-in-time stories. The thing to realize here is that the idler photon measurement and the screen photon landing position are
correlated. If I tell you one, I've also told you something about the other. But remember:
correlation is not causation. This age-old statistical advice is even more important to remember when it comes to quantum mechanics, because QM has a surprisingly counter-intuitive kind of correlation (i.e. entanglement). Is the screen photon causing the idler photon's rotation? Is the idler photon causing the screen photon to be in a wavy pattern? No. Both of those ways of thinking are misleading. The photons are merely correlated.
All that being said, it helps to take a step back, stop focusing on the flickery noise of the individual runs, and just look over the conditional expectations:
This isn't some magic time-defying experiment. It's not even inherently quantum; you can easily create analogous classical experiments. The quantum part is just there to mask the fact that we're confusing correlation for causation.
But practically, you need either to get some grasp of QM or to find a really good explanation for the beginners of this particular experiment of Kim. Otherwise I do not see how these things can be understood.
