Understanding Retrocausality and Blockworld

In an Insights series “Blockworld and its Foundational Implications,” I quoted Huw Price and Ken Wharton in several places advocating a blockworld approach to physics (called the Lagrangian Schema[1]). While Ken did sign off on my use of these quotes, I wasn’t entirely fair to the Price & Wharton program because I didn’t reveal their motive, i.e., retrocausality. In this Insight, I want to rectify that omission and briefly show how they and others are using retrocausality to deal with the conundrums of quantum nonlocality. Before I begin, let me first say that this is not a sales pitch for retrocausality, it is merely a brief introduction thereto. Thus, second, I’m not going to argue for or against any particular approach to retrocausality. Third, the research programs I will briefly introduce herein have been well-established in the foundations of physics community through the peer-review process, as evidenced by the references herein from Physical Review Letters, Physical Review A, Physical Review D, and Reviews of Modern Physics. With those caveats, let me begin.

Retrocausality is best understood in its many explanatory applications and instantiations, the breadth of which makes it difficult to define precisely, but loosely speaking retrocausality is an attempt to explain quantum nonlocality using future boundary conditions plus an experimentalist’s ability to intervene. Let me unpack that a bit.

The term “quantum nonlocality” is used to mean different things, but here I use it as defined in Wikipedia[2], “the phenomenon by which measurements made at a microscopic level contradict a collection of notions known as local realism that are regarded as intuitively true in classical mechanics.” One of the aspects of local realism I discussed in part 5 of my Insights series on blockworld was counterfactual definiteness, i.e., an object possesses properties that are not dependent upon whether or not a measurement is made to reveal those properties. For example, whether or not I’m wearing blue pants is not dependent upon you or anyone else looking to see what pants I’m wearing. In the Hardy experiment, I showed how counterfactual definiteness is called into question in a run producing a 22GG outcome. In that case, we weren’t able to tell a time-evolved story of the particles with definite properties R or G for both possible measurements 1 and 2 from emission to detection without violating locality (no superluminal signaling, i.e., no information traveling on space-like paths). I equated counterfactual definiteness with “realism” in that article and stated that experiments like this had caused most in the foundations community to question counterfactual definiteness (realism) so as to preserve locality. But there is a loophole in the argument I presented, i.e., I didn’t allow for the possibility that information about measurement settings might come from the future on time-like paths, thereby maintaining another form of locality-preserving realism, i.e., a fact of the matter about the physical situation in the spacetime region between emission and detection events whereby information travels on time-like paths. This loophole is called “retrocausality” and the means by which the particles involved might have access to information about the future is a “future boundary condition.” As far as “intervention” is concerned, I will dodge the murky waters of a free will discussion and simply quote Price & Wharton[3]:

… the retrocausal proposal accepts the standard presupposition of all experimental science, namely that experimenters such as Alice and Bob are free to choose measurement settings. Moreover, it accepts a standard operational definition of causality – a definition long assumed in science, and refined and formalised in philosophy over the past three decades – in which the notion of free agency plays a central role. According to this so-called “interventionist” account of causality, a variable X is a cause of a variable Y if and only if a free intervention on X makes a difference to Y.

Accordingly, in the Hardy experiment per the “interventionist” account of causality, Alice and Bob’s choices of measurement setting 2 for the outcome 22GG can be viewed as a “cause” of the particles’ R-G property at emission. This “retrocausality” negates the need for counterfactual definiteness altogether, since the measurement settings and outcomes are ‘known’ by the particles at emission. However, there is still an ontological fact of the matter in the spacetime region between the emission and detection events, so retrocausality allows for realism without violating locality.

While this does not do justice to the many other motives for pursuing retrocausality in its many instantiations, this Insight is only intended as a brief introduction. Accordingly, I now provide examples of three different approaches to retrocausal explanation which are, broadly speaking: retro-time-evolved causal stories in the blockworld, global contraints in a blockworld, and an evolving blockworld or a growing causal set (causet). These examples are certainly not exhaustive, but provide a general overview of retrocausal approaches.

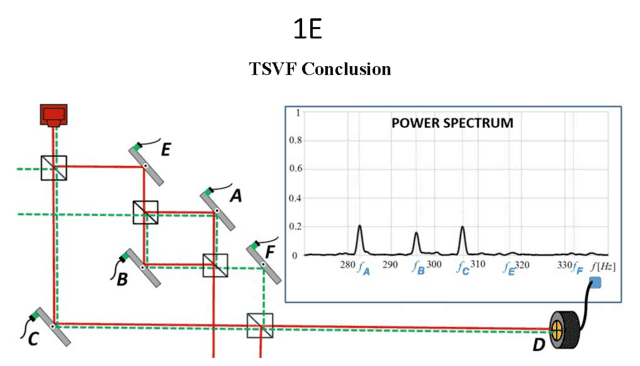
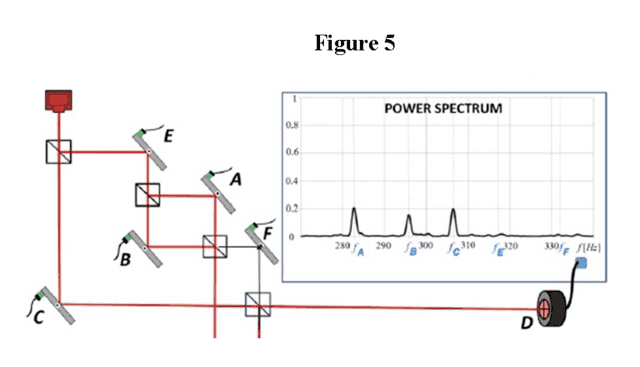
As an example of retro-time-evolved causal explanation in a blockworld, consider the Two-State Vector Formalism (TSVF). In the TSVF formulation of quantum mechanics (QM), the quantum state $\langle \Phi \mid$ evolves backward in time from the measurement event and the quantum state $\mid \Psi \rangle$ evolves forward in time from the emission event, so causation occurs in both temporal directions. This formulation of QM is used in the computation of “weak values”[4] where $\langle \Phi \mid$ is called the “post-selected state” and $\mid \Psi \rangle$ is called the “pre-selected state.” A “weak” interaction is then introduced between the state and the experimental equipment where “weak” means the interaction can be approximated accurately as a linear perturbation that doesn’t actually lead to a collapse of the wave function. A weak measurement is therefore viewed as a noninvasive probe of the quantum system. For example, consider the experiment by Danan, Farfurnik, Bar-Ad, and Vaidman (DFBV)[5], “Asking Photons Where They Have Been” as shown in their Figures 1A – E below (with their captions). In the configuration of Figure 1A, constructive interference obtains through the outer and nested interferometers from the Source to detector D. In the configuration of Figure 1B, mirror B is moved so that destructive interference obtains between the nested interferometer and mirror F. The weak measurement is the interaction between the vibrating mirrors and the quantum system where the vibratory amplitude of the mirrors is small (weak) enough so that the probability amplitude can be computed using the first-order terms of the full wave function (as shown in their Appendix and by Saldanha[6]). Evidence of this weak interaction is then found in the frequency distribution of the photons on the face of detector D. The results of the various experimental configurations are shown in their Figure 1 below. The question is of course, how is it that information about the vibratory frequencies of mirrors A and B gets to detector D in the configuration of Figure 1B? And, if information about mirrors A and B gets to detector D, why not information about mirrors E and F? Their ontological answer, as shown in their Figure 1E below, is the mirrors that are connected to both the Source and detector D by forward and backward time-evolving waves are the ones that convey vibratory information. The backward time-evolving wave, i.e., the retrocausal wave, is just as important causally as the forward time-evolving wave.

Their experiment can be explained by classical electromagnetism[6], as DFBV point out, and I’m not trying to sell their interpretation, but it provides an excellent example of retro-time-evolved causal explanation. In this case, even though it’s a blockworld (outcomes must already ‘exist’ when the photons are emitted, since information about their detection is available at the emission event), the authors tell a time-evolved causal story (both forward and backward in time). As Price points out[7], such time-evolved stories in a blockworld are “perspectival” from within the blockworld. Certainly there is nothing wrong with telling dynamic stories in a blockworld, such stories harmonize with our dynamic, time-evolved experience and they are accommodated in the vast majority of cases. In this particular retrocausal explanation, the authors simply tell a causal story that proceeds in both temporal directions.

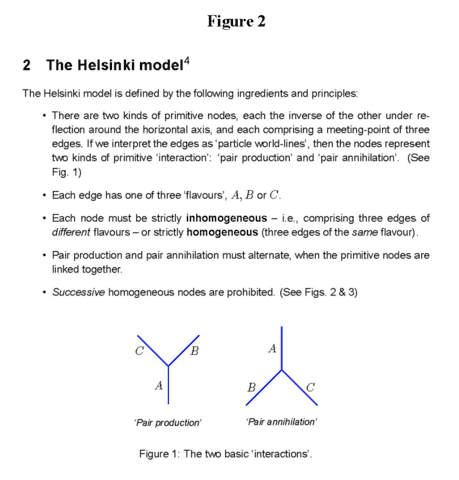
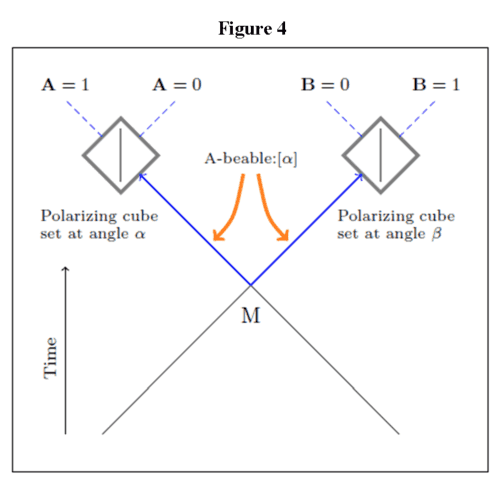
Of course, in a blockworld you can dispense with time-evolved causal stories altogether if you rather provide an adynamical ‘causal mechanism’ (global constraint), and the DFBV experiment is no exception. According to the Relational Blockworld explanation of the DFBV experiment[8], there is no photon or wave moving through the interferometer either forward or backward in time. Rather, there is a spacetimesource element spanning the interferometer from emission to detection (like the red line in Figure 1A) and it is responsible for the transfer of energy from the Source to detector D. The probability amplitude for the spacetimesource element is then determined by an adynamical global constraint. In Price’s Helsinki toy model paper[9] (Figure 2) he “shows how something that ‘looks like’ retrocausality can emerge from global constraints on a very simple system of ‘interactions’, when the system in question is given a natural interpretation in the light of familiar assumptions about experimental intervention and observation.” And Wharton has introduced a toy model[10] using only a Lagrangian, i.e., no dynamic laws, to model the quantum state. According to Wharton’s explanation of the DFBV experiment, given the detection of a full photon at D, no intermediate classical (Maxwell) field trajectory is available. But a minimally-non-classical or “anomalous” field history is available by introducing a relative phase shift between the two arms of the central interferometer (at A or B, or both A and B). Generally, a corresponding phase shift must also occur at C, so that the fields coherently combine at the final beam splitter. Such intermediate phase anomalies must occur for any D-detection, whether the mirrors are vibrated or not, but given an external noise source at the mirrors, this noise is the least unlikely way to generate the necessary anomalies (as revealed in the output spectrum). Noise at E or F does not contribute to any useful phase anomalies in this “all at once” (block-universe-retrocausal) analysis of a minimally-non-classical field that leaves A and fully arrives at D. This version of the Lagrangian Schema was spawned when Wharton, Miller & Price[11] and Evans, Price & Wharton[12] noticed that the action for experiments possessing time-like separated outcomes without quantum nonlocality (Figure 3) and the action of experiments possessing space-like separated outcomes with quantum nonlocality (Figure 4) are related by a simple spacetime transformation. Since the actions are dual in this sense, they argue that the ontology is equivalent in the same sense, i.e., the Feynman Integral Symmetry Hypothesis[11]:

For any two experiments with an action duality (a well-defined spacetime transformation that maps the classical Lagrangian density of one experiment onto the classical Lagrangian density of the other), any realistic ontology must also map between the two experiments under the same spacetime transformation.

Again, as Price points out, one can still tell a retro-time-evolved causal story in a blockworld, so the use of a global constraint to characterize how information is distributed in the blockworld falls in the retrocausality camp.

A prominent example of this versatility in explanation is provided by Cramer’s Transactional Interpretation (TI) [13]. Therein Cramer uses advanced waves from detection events to emission events called “confirmation waves” $\langle \psi \mid$, and he uses retarded waves $\mid \psi \rangle$ called “offer waves” that proceed from emission events to detection events. The combination of the two waves forms a “transaction” responsible for the exchange of energy-momentum associated with a particle. This causal explanation is temporally bi-directional like TSVF, using a blockworld with future boundary conditions and intervention, so it’s an example of a retro-time-evolved causal story. However, Cramer says the backwards-causal elements of his theory are “only a pedagogical convention” and that in fact “the process is atemporal,” as with the adynamical explanation of a global constraint. Again, either explanatory mechanism, adynamical global constraint or retro-time-evolved causal story, can be used with TI.

This leads us to the third type of retrocausal explanation characterized by Elitzur & Dolev’s belief[14] “that genuine change, not static geometry, is reality’s most basic property,” so that “Perhaps, rather, spacetime itself is subject to evolution.” Kastner[15] embraces a similar notion with her growing causet version of TI called the Possibilist Transactional Interpretation (PTI). The reason these approaches are retrocausal is that the evolution of the blockworld or the growth of the causet doesn’t proceed strictly from past to future, but the present along any worldline evolves, in part, according to future boundary conditions that allow for intervention. In PTI, the offer and confirmation waves exist in “pre-spacetime” and a spacetime network/graph grows out of actualized transactions in a robust sense. Kastner writes[16]:

The possibilist transactional picture can be viewed as a physical basis for the emergenceof the partially ordered set of events in the causal set formalism. This formalism is currently being explored as a means to constructing a satisfactory theory of quantum gravity, and it has much promise in that regard. However, even apart from general relativistic considerations, the formalism breaks new ground in showing that, contrary to a well-entrenched belief, a block world ontology is not required for consistency with relativity. The causal set structure is a ‘growing universe’ ontology which nevertheless preserves the relativistic prohibition on a preferred frame.

PTI and TI have the following in common with the TSVF approach:

1. The post-selection is a crucial part of the ontology.
2. The photon is necessarily described by both the offer wave and the confirmation wave (the latter resulting from the post-selection).

According to a PTI/TI analysis of the DFBV experiment, the offer wave reaching detector D has two degrees of freedom, as discussed by Saldanha[6], and per that full physical description the forward time-evolving offer wave is connected to both the Source and detector D through the additional transverse degree of freedom (Figure 5). Thus, unlike TSVF and Relational Blockworld, there is no discontinuity of the photon path in the PTI/TI account of the DFBV experiment.

Some years ago I was talking to Aharonov about the value of QM interpretations. He said physics doesn’t care about interpretations unless they can inspire new experiments and new ways to approach physics. Retrocausality certainly satisfies that requirement.

FIG. 1: (A) Measured power spectrum of the signal from the quad-cell photo detector shows frequencies of oscillation of all internal mirrors of the interferometer. (B) When the inner interferometer is tuned in such a way that the beam of light passing through it does not reach the photo-detector, the power spectrum of the signal in the photo-detector still shows frequencies of the mirrors of this inner interferometer. (C) These frequencies (and all other signals) disappear when we, without changing anything in the upper arm, block the lower arm of the large interferometer.

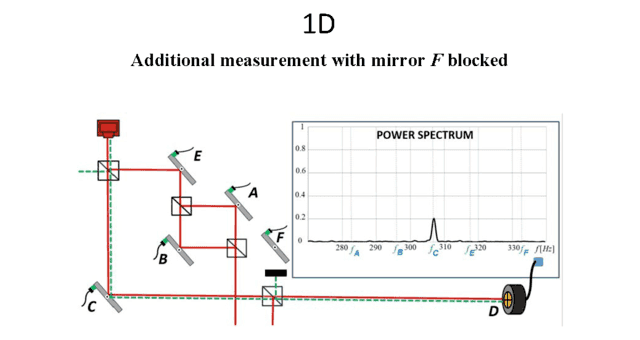
FIG. 1D: The forward and backward evolving states are present together only at mirror C and thus, the only peak in the power spectrum is at f_C. Since according to the naïve approach the presence of peaks at f_A and f_B in Figure 1B is very counterintuitive, one might suspect that these peaks may result from some unrelated electronic noise. A block between mirror F and the last beam splitter absorbs the backward evolving wave moving towards mirrors F, A, B, and E. In the language of the forward wave function only, it absorbs the leakage of the wave from the inner interferometer. Thus theoretically, according to the standard and the TSVF approaches, the block ensures the absence of peaks at the corresponding frequencies. Therefore, this experiment provides a decisive test for the absence of electronic noise in Figure 1B.

FIG. 1E: The two-state vector description of the photon inside the interferometer includes the standard forward evolving quantum state (red line) and the backward evolving quantum state (green dashed line) of the photon detected by the quad-cell photo-detector. It provides an explanation of the observed power spectrum: frequencies f_C, f_A, and f_B are present while f_E and f_F are not. The photon was present only where both forward and backward quantum wave functions do not vanish.

 

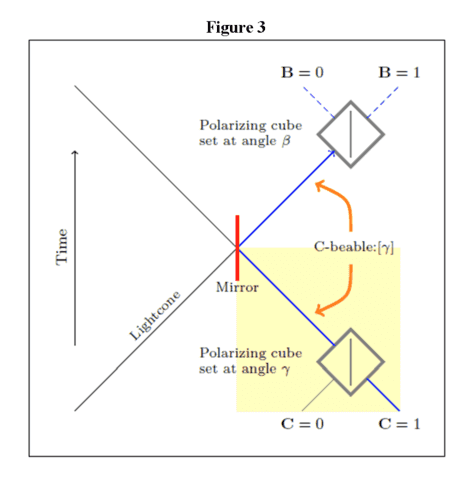The outcome at cube B is related to the setting of cube C by time-like paths with information always flowing forward in time.

The outcome at cube B is related to the setting of cube A by time-like paths, but the information flow is retrocausal from A to M.

Fig 1B of DFBV modified to show the transverse component of the forward time-evolving offer wave from the nested interferometer through mirror F reaching detector D.

1. Wharton, K.: The Universe is not a Computer. In Questioning the Foundations of Physics, A. Aguirre, B. Foster and Z. Merali (Eds), pp.177-190, Springer (2015) http://arxiv.org/abs/1211.7081. This essay won third prize in the 2012 FQXi essay contest.
2. https://en.wikipedia.org/wiki/Quantum_nonlocality
3. Price, H., & Wharton, K.: Disentangling the Quantum World. Entropy 17, 7752-7767 (2015) http://arxiv.org/abs/1508.01140.
4. Aharonov, Y., Albert, D., & Vaidman, L.: How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Physical Review Letters 60, 1351-1354 (1988); Duck, I., Stevenson, P., & Sudarshan, E.: The sense in which a ‘weak measurement’ of a spin-1/2 particle’s spin component yields a value 100. Physical Review D 40, 2112–2117 (1989); Ritchie, N., Story, J., & Hulet, R.: Realization of a measurement of a ‘weak value’. Physical Review Letters 66, 1107–1110 (1991); Dressel, J., Malik, M., Miatto, F., Jordan, A., & Boyd, R.: Colloquium: understanding quantum weak values: basics and applications. Reviews of Modern Physics 86, 307–316 (2014).
5. Danan, A., Farfurnik, D., Bar-Ad, S., & Vaidman, L.: Asking Photons Where They Have Been. Physical Review Letters 111, 240402 (2013) http://arxiv.org/abs/1304.7469.
6. Saldanha, P.: Interpreting a nested Mach-Zehnder interferometer with classical optics. Physical Review A 89, 033825 (2014) http://arxiv.org/abs/1312.7438.
7. Price, H.: Causal perpectivalism. http://philsci-archive.pitt.edu/4475/1/TimeAsymmetryOfCausation.pdf (2005).
8. Stuckey, W.M., Silberstein, M., & McDevitt, T: Relational Blockworld: Providing a Realist Psi-Epistemic Account of Quantum Mechanics. International Journal of Quantum Foundations 1, 123-170 (2015) http://www.ijqf.org/wps/wp-content/uploads/2015/06/IJQF2015v1n3p2.pdf.
9. Price, H.: Toy models for retrocausality. Studies in History and Philosophy of Modern Physics 39 (4), 752-761 (2008).
10. Wharton, K.: Quantum States as Ordinary Information. Information 5(1), 190-208, doi:10.3390/info5010190 (2014) http://www.mdpi.com/2078-2489/5/1/190.
11. Wharton, K., Miller, D.J., & Price, H.: Action Duality: A Constructive Principle for Quantum Foundations. Symmetry 3, 524-540 (2011) doi:10.3390/sym3030524 http://arxiv.org/abs/1103.2492.
12. Evans, P., Price, H., & Wharton, K.: New Slant on the EPR-Bell Experiment. British Journal for the Philosophy of Science 64, 297-324 (2013) http://arxiv.org/pdf/1001.5057.pdf.
13. Cramer, J: The transactional interpretation of quantum mechanics. Reviews of Modern Physics 58, 647-687 (1986).
14. Elitzur, A., & Dolev, S.: Quantum Phenomena within a New Theory of Time. In: Elitzur, A., Dolev, S., & Kolenda, N. (eds.) Quo Vadis Quantum Mechanics? pp 325-349, Springer, Berlin Heidelberg (2005).
15. Kastner, R: The Transactional Interpretation of Quantum Mechanics: The Reality of Possibility. Cambridge University Press, New York (2013).
16. Kastner, R.: The Emergence of Spacetime: Transactions and Causal Sets. Forthcoming In: Licata, I (ed.) The Algebraic Way: Space, Time and Quantum Beyond Peaceful Coexistence, Imperial College Press, London (2015) http://arxiv.org/abs/1411.2072.