Blockworld and Its Foundational Implications: Time Dilation and Length Contraction

 

This is the first in a 5-part series of Insights that will introduce blockworld (aka “block universe”) and use it to address a puzzle (origin of the universe), paradoxes[1] (of closed timelike curves), and conundrums[2] (of quantum nonlocality) that I have seen discussed on Physics Forums. Blockworld (BW) says the past, present and future are equally ‘real’, i.e., they co-exist on equal footing. This is contrary to our experience whereby only the present exists, the past no longer exists and the future is yet to exist. It’s certainly not the case that BW must be used to resolve the puzzle, paradoxes and conundrums herein, I’m only showing that it can be used to do so.

In this first Insight, I will explain time dilation (“moving clocks run slow”) and length contraction (“moving objects shrink”) per special relativity (SR). Accordingly, if you and observers at rest with respect to you (hereafter simply “you”) see me moving, you should see me aging more slowly than you. But motion is relative, so I (and observers at rest with respect to me) say you’re the ones moving and therefore we should see you aging more slowly than us. In the second Insight, I will explain how the relativity of simultaneity resolves this paradox, but at the cost of BW. Here’s a nice quote from Geroch[3] that captures the BW perspective:

There is no dynamics within space-time itself: nothing ever moves therein; nothing happens; nothing changes. In particular, one does not think of particles as moving through space-time, or as following along their world-lines. Rather, particles are just in space-time, once and for all, and the world-line represents, all at once, the complete life history of the particle.

In the third Insight, I will (conceptually) introduce general relativity (GR) and bring the BW perspective to bear on general relativistic cosmology to ‘explain’ what puzzles so many people about big bang cosmology, i.e., the origin of the universe. The answer will not be satisfying for those who want an answer in terms of a time-evolved (dynamical) story. The answer is that the origin of the universe (big bang) is just one point in the BW and as such its existence is no more mysterious than any other point in the BW. The reason the existence of the big bang seems mysterious is that a dynamical story about the universe traced backwards in time ends at the big bang. The state of the universe at any given time $\tau$ is explained dynamically by time evolving the state of the universe at the time immediately preceding $\tau$. Finding and using the laws that govern time evolution form the basis of dynamical explanation. Since there is no time preceding the big bang, it cannot be explained dynamically. The key to avoiding this explanatory problem is to relegate dynamical explanation based on time-evolved states to secondary (non-fundamental) status and accept that the more general BW explanation based on an adynamical, spatiotemporally global constraint (rather than laws of motion) is truly fundamental. In this more general BW explanation, Einstein’s equations are understood adynamically as a global constraint. I will address this further in part 3 of this series. In the fourth Insight, I will bring this adynamical view of GR and BW to bear on the paradoxes of closed timelike curves. Finally, in the series conclusion, I will bring this general idea of BW explanation based on adynamical global constraints to bear on the conundrums of quantum nonlocality, i.e., delayed choice and no counterfactual definiteness. So, let me get this whole process started!

I will start with the postulates of SR and then show how the second postulate leads to time dilation and length contraction. The postulates of SR are http://www.nobelprize.org/educational/physics/relativity/postulates-1.html:

1. The Principle of Relativity – The laws of physics are the same in all inertial frames of reference.
2. The Constancy of Speed of Light in Vacuum – The speed of light in vacuum has the same value c in all inertial frames of reference.

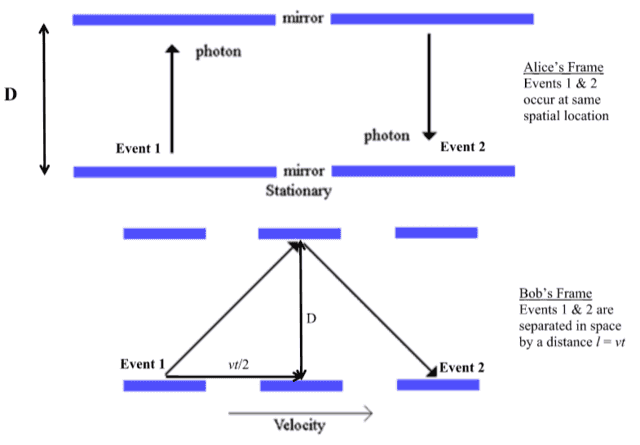
First suppose that a light pulse bounces back and forth between mirrors separated by a distance D (top half of Figure 1). Alice, at rest with respect to the mirrors, measures a time T for the light pulse to leave from the bottom mirror (Event 1), bounce off the top mirror, and return to the bottom mirror (Event 2). Thus, Alice says

\begin{equation} c = \frac{2D}{T}  \label{Alice1} \end{equation}

Now suppose Alice is moving to the right with respect to Bob at speed v. Bob measures a time t between Events 1 & 2 with the light pulse taking the path shown in the bottom half of Figure 1. Since everyone measures the same speed of light, Bob computes

\begin{equation} c = \frac{2\sqrt{D^2 + \frac{v^2t^2}{4}}}{t}  \label{Bob1} \end{equation}

Solving for t(T) we find

\begin{equation} t = \frac{T}{\sqrt{1 – \frac{v^2}{c^2}}}  \label{time1} \end{equation}

T is called the “proper time” between Events 1 & 2 because those two events occur at the same location in space for Alice. For Bob, those two events occur at two different locations in space and his time t is longer than the proper time T. That observers measure the time between events occurring at two different locations in space to be longer than the proper time between those events is called “time dilation.” Thus, Bob says Alice’s clock runs slow. Of course since motion is relative, it must also be the case that Alice says Bob’s clocks run slow compared to hers. I’ll explain how SR allows these seemingly contradictory facts to hold in part 2 of this series. I will say now that the resolution of this paradox has nothing to do with the time delay of light in getting from one point to another, i.e., it’s not an optical illusion, all measurements will be made locally. Finally, let me introduce length contraction.

Suppose Alice is crashing through two walls at rest with respect to Bob at Events 1 & 2. These walls are separated by a distance l = vt according to Bob. Motion is relative, so Alice says Bob is moving to the left at speed v, i.e., they must agree that their relative speed is v. Since Alice says the time T between Events 1 & 2 is shorter than the time t that Bob says passes between Events 1 & 2 by a factor of $\sqrt{1 – \frac{v^2}{c^2}}$, Alice must therefore also say her distance L between the walls of Events 1 & 2 is shorter than Bob’s distance l by the same factor, i.e.,

\begin{equation} l = \frac{L}{\sqrt{1 – \frac{v^2}{c^2}}}  \label{length1} \end{equation}

Bob measures what is called the “proper length” between the walls, since he is at rest with respect to the walls, so Alice measures a shorter length than the proper length. That observers in motion with respect to an object measure its length to be shorter than its proper length is called “length contraction.” Thus, Alice says Bob’s meter sticks are shorter than one meter. Of course since motion is relative, it must also be the case that Bob says Alice’s meter sticks are shorter than one meter. I’ll explain how SR allows these seemingly contradictory facts to hold in the next (second) Insight of this series.

Figure 1

Modified From “Photon Clock” at Contemplicity.com http://www.contemplicity.com/home/essays-the-ever-changing-history-of-the-universe/attachment/1

1. “a statement that is seemingly contradictory or opposed to common sense and yet is perhaps true” http://www.merriam-webster.com/dictionary/conundrum

2. “a question or problem having only a conjectural answer” http://www.merriam-webster.com/dictionary/conundrum

3. Geroch, R.: General Relativity from A to B. University of Chicago Press, Chicago (1978), pp 20-21.

Note: Comments for this post have been disabled. Please show your feedback by using the star rating at the top of the article and or contacting the author personally.