Kinematics: Distance and time with limited acceleration and deceleration

[MMCS]

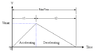
a motorcycle starts from rest point A and travels 300m along a straight horizontal track to point B where it comes to a stop. if the acceleration is limited to 0.7g and deceleration to 0.6g calculate the least possible time to cover the distance and maximum velocity reached.

Can anyone point me in the right direction? i don't know where to start with this as the distance traveled at acceleration and deceleration is not defined and as they are not the same i assume you can't divide the distanc by 2

Thanks

 

[tiny-tim]

Welcome to PF!

Hi MMCS! Welcome to PF!

Call the two distances s₁ and s₂ …

you know they have to add to 300 …

then get two standard constant acceleration equations (one with a = 0.7 and one with a = -0.6), combine them with s₁ and s₂ = 300, and solve

 

[MMCS]

Thanks!

Could you possible reccomend a formula to use, i can't find one that includes distance, time and acceleration without velocity and i can't use velocity because S1 has an U value of 0 but an unknown V and visa versa for S2, leaving 2 unknows in each equation t and u or v

 

[tiny-tim]

Hi MMCS!

Surely you know a constant acceleration equation using only a u s and t ?

 

[MMCS]

Sorry I am new to this:

if i was to use this formula v2 = u2 + 2as for say S1 what whould i use as the distance as 300 is the distance for S1 and S2

also i have tried to use this one s = ut + 1/2 at^2

S1 = 0t + 1/2 x 6.9 x t^2

S2 = ut + 1/2 x 5.9 x t^2

S1 + S2 = 300

3.45 x t^2 + -2.95 x t^2 + ut = 300

0.5 x t^2 + ut = 300

300/0.5 = t^2 + ut

600 = t^2 + ut

Because i don't know U for s2 i have 2 unknowns so i can't solve it

 

[tiny-tim]

Because i don't know U for s2

ah, but you know V for s₂ instead (and a s and t)

 

[MMCS]

Where can i use V?

 

[tiny-tim]

in s = ut + 1/2 at² …

you can either use negative t (so your "start time" is 0, and your "end time" is -t),

or if you prefer you can memorise the alternative formula:

s = vt - 1/2 at² ​

 

[MMCS]

So we have

S1 = 0t + 1/2 x 6.9 x t^2

S2 = 0t - 1/2 x - 5.9 x t^2

S1 + S2 = 300

3.45 x t^2 + 2.95 x t^2 + ut = 300

6.4 x t^2 = 300

300/6.4 = t^2

46 = t^2

sqrt46 = t

6.85 = t

However i have 13.76s as the answer in my booklet? Have a gone wrong anywhere?

Thanks for your help, hopefully iv nearly got it!

 

[gneill]

One small problem -- you've assumed that the time intervals for acceleration and deceleration are equal. That is, you've used the same variable, t, for both the acceleration time and the deceleration time. This is unlikely to be true as the accelerations are not equal in magnitude.

 

[MMCS]

So there would have to be separate functions for t1 and t2? How would i get them?

 

[gneill]

So there would have to be separate functions for t1 and t2? How would i get them?

Study the diagram that I posted above. What are the slopes of the line segments making up the velocity vs time function? Can you determine a relationship between t1 and t2?

 

[tiny-tim]

you have to minimise t₁ + t₂, given that they satisfy a equation of the form At₁² - Bt₂² = C

there are various ways of doing this: one would be to write the thing you have to minimise (t₁ + t₂) as P (and maybe chuck in (t₁ - t₂) as Q)