Kinematics -- Projectile motion problem

[MARK 42]

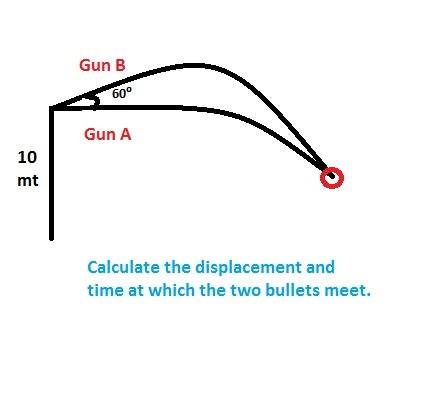
One bullet was fired from Gun A and Gun B each at varying time interval. Both the guns are 10 meters above the ground. Calculate: a) Which gun was fired first. b) Displacement and time at which the two bullets will collide.

 

[Bystander]

What have you done so far? Just the vertical displacement? Or, both vertical and horizontal displacements?

 

[RUber]

First off, you did not use the template. Please do.
Secondly, you have not shown your efforts yet.
Lastly, you should be able to answer at least part a based on your intuition. I guess the assumption is that the firing velocity of both guns is equal.

 

[MARK 42]

Oh, sorry.
If we consider time as 'T' then by traditionally solving, I got Ta = 1/2Tb. I don't know what to do further. The final answer is 1 second.
And the displacements, I got Sy for A=Sy for B.

 

[RUber]

1 second for Ta or Tb?
I am guessing that trajectory a starts completely horizontal, and b is at 60 degree elevation from horizontal.

Next, you should relate the y displacement positions at the final time:
$v\frac{\sqrt{3}}{2}T_f - \frac{9.8}{2}(T_f)^2 = - \frac{9.8}{2}\left(\frac{T_f}{2}\right)^2$

I don't immediately see how you can find a solution without some dependence on initial velocity, unless you knew T_f =1 sec from the start.

 

[MARK 42]

Exactly. I feel the same. I think the question somehow lacks specifications with respect to both velocity and time.
Anyways, thanks for your help.

 

[mfb]

I can confirm that you need one of them. Otherwise doubling the velocity and the time difference for a solution scales everything up and leads to a new solution.

 

[MARK 42]

What if we consider initial velocity = 0? Assuming the calculation starts from the point the bullets were at rest?

 

[mfb]

You can't have a horizontal motion or a 60° angle if you release the bullets at rest. Also, they will never meet then.

Actually, I wonder why the 10 meters are given, they don't seem relevant.
If you assume that the bullets hit each other at the same time they hit the ground, the problem gets a unique solution (assuming the initial velocities are the same).

 

[MARK 42]

Our teachers modified the question giving us the velocity as 5√3 m/s. Would that work?

 

[mfb]

Sure.

 

[RUber]

Did you find a solution?