asdf12312
- 198
- 1
Kinetic energy of ball sliding down slope with electric field??
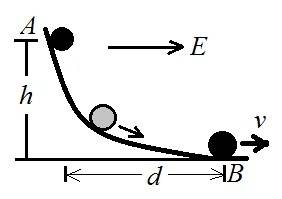
As shown in the figure above, a positively charged ball is placed at point A and slides down the slope from rest. The area has a uniform electric field E = 26.1 N/C, pointing to the right. The mass of the ball is m = 27 kg and the charge is q = +4.6 C. When the ball reaches point B, it travels horizontally there after. The height from A to B is h = 23 m and the horizontal distance between A and B is d = 47 m. You can ignore friction and use g = 10 m/s2 for your calculation.
1. How much is the kinetic energy of the ball when it reaches at B (in the unit of J)?
2. If the electric field is changed to the opposite direction, How much is the kinetic energy of the ball when it reaches at B (in the unit of J) now?
3. What is the minimum strength of electric field E that can be used to stop the particle right at Point B?
probably need to use Ke = qEd ..? i tried but getting the wrong answer. for d i calculate using pythorean x^2+y^2=d^2 so 23^2+47^2=d^2 is that rite way to do?
Homework Statement
As shown in the figure above, a positively charged ball is placed at point A and slides down the slope from rest. The area has a uniform electric field E = 26.1 N/C, pointing to the right. The mass of the ball is m = 27 kg and the charge is q = +4.6 C. When the ball reaches point B, it travels horizontally there after. The height from A to B is h = 23 m and the horizontal distance between A and B is d = 47 m. You can ignore friction and use g = 10 m/s2 for your calculation.
1. How much is the kinetic energy of the ball when it reaches at B (in the unit of J)?
2. If the electric field is changed to the opposite direction, How much is the kinetic energy of the ball when it reaches at B (in the unit of J) now?
3. What is the minimum strength of electric field E that can be used to stop the particle right at Point B?
Homework Equations
The Attempt at a Solution
probably need to use Ke = qEd ..? i tried but getting the wrong answer. for d i calculate using pythorean x^2+y^2=d^2 so 23^2+47^2=d^2 is that rite way to do?
Last edited: