Checking My Understanding of a Magnetic Circuit: Help Appreciated!

[jisbon]

Homework Statement

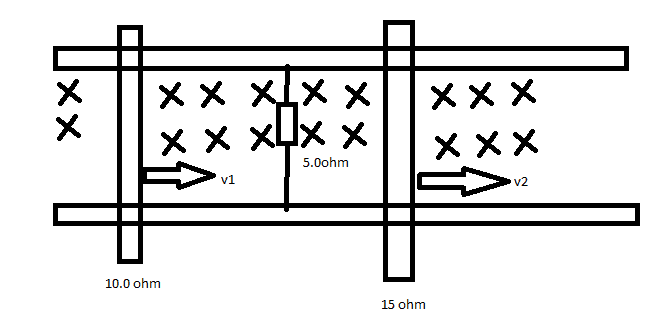
Two parallel rails with negligible resistance are 10.0 cm apart and are connected by a 5.00 resistor. The circuit also contains two metal rods having resistances of R = 10.0Ω and 15.0 Ω sliding along the rails. The rods are pulled to the right at constant speeds 4.00 m/s and 2.00m/s, respectively. A uniform magnetic field of magnitude 0.0100 T is applied perpendicular to the plane of the rails. Determine the magnitude and direction of the current in the 5.00 Ωresistor

Relevant Equations

I'm not totally sure on this.

So I was checking this question out, and I saw that someone did discuss about a similar question before on this forum here:

https://www.physicsforums.com/threads/did-i-get-it-right-by-coincidence.487088/
Since this is a different question, I would like to ask if anyone here could help me check my equation from my understanding (or at least what I thought), here is the diagram:

So applying junction rule,

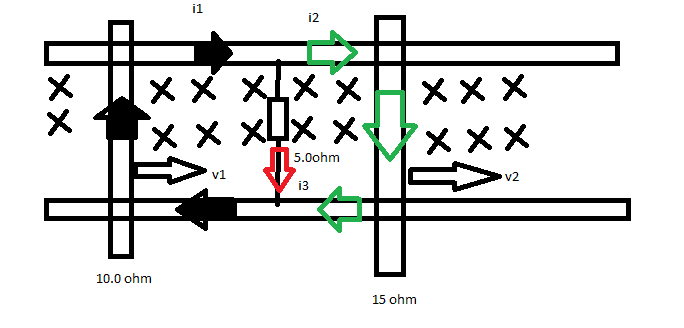
Black arrow = I1
Green arrow = I2
Red arrow = I3
$$I1= I2+ I3$$

Now applying the other rule aka the loop rule:

My left loop will be:

$$-I1(10) - I3(5) - BLV1 = 0$$

?

My right loop will be:

$$I2(15)-I3(5)-BVL2 = 0$$

?

I'm not entirely sure how the loop goes about when there's a magnetic field (only dealt with them in normal circuits), so any assistance will be greatly appreciated. Cheers!

 

[scottdave]

It is the changing magnetic field which induces a voltage. See this - http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html

 

[rude man]

EDIT:
Actually, I see nothing wrong with what you attempted to do but I don't use the KCL law so there may be a sign error or two but otherwise it looks fine. Did you compute I1, I2 & I3?
EDIT2 - I ran the computations and at least if the 15 ohm → ∞ and v2=0 the answer came out right.

 

[jisbon]

EDIT:
Actually, I see nothing wrong with what you attempted to do but I don't use the KCL law so there may be a sign error or two but otherwise it looks fine. Did you compute I1, I2 & I3?
EDIT2 - I ran the computations and at least if the 15 ohm → ∞ and v2=0 the answer came out right.

Sorry, but what do you mean if 15 ohm → ∞ ? Not sure about that. Oh and v2= 2.00m/s

 

[jisbon]

It is the changing magnetic field which induces a voltage. See this - http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html

Yep, I saw the part where faraday's law states that a changing magnetic field will produce voltage, hence EMF=BLV , however, I'm still unclear for the direction. If magnetic field is pointing in and rods are moving to the right, will it mean that the current will go clockwise direction using right hand grip rule? Thanks

 

[rude man]

Sorry, but what do you mean if 15 ohm → ∞ ? Not sure about that. Oh and v2= 2.00m/s

I just solved a simpler problem as a quick reality check, with no 15 ohm resistor present. I could do the same for the 10 ohm & then use superposition. So could you.

 

[rude man]

Yep, I saw the part where faraday's law states that a changing magnetic field will produce voltage, hence EMF=BLV , however, I'm still unclear for the direction. If magnetic field is pointing in and rods are moving to the right, will it mean that the current will go clockwise direction using right hand grip rule? Thanks

Use Lenz's law. Which polarity of current applies a resisting force to the motion?

 

[jisbon]

Use Lenz's law. Which polarity of current applies a resisting force to the motion?

I'm assuming the motion refers to the movement of the rods being pulled to the right? So if I use right hand rule , magnetic field points in, force points towards right, current points up (aka clockwise?) and Lenz's law states that an induced electromotive force (emf) always gives rise to a current whose magnetic field opposes the change in original magnetic flux, so current will be anticlockwise?

 

[rude man]

BTW I suggest use of software to solve your three equations. It turned out surprisingly messy.
Also, I suggest replacing the 5ohm with R1, the 10ohm with R2 and the 15ohm with R3. Makes computation easier and allows you to do dimensional checking which should be part of every problem solving.

 

[jisbon]

BTW I suggest use of software to solve your three equations. It turned out surprisingly messy.
Also, I suggest replacing the 5ohm with R1, the 10ohm with R2 and the 15ohm with R3. Makes computation easier and allows you to do dimensional checking which should be part of every problem solving.

What software are available to use? And is my understanding correct as shown above? Would like to check that. Thanks

 

[rude man]

What software are available to use? And is my understanding correct as shown above? Would like to check that. Thanks

As I said I know your approach is correct and your equations probably are also except for possible sign mistakes (I'm too lazy to check). And yes, the current is clockwise.
Software: I use a very antiquated software called Derive, in its original DOS (floppy disc!) version, which means I have to execute on my XP machine. I think MathCad is a modern one but there are dozens out there that can solve simultaneous algebraic equations.