BOAS
- 546
- 19
Hello,
I thought I had questions concerning Kirchoff's rules down to a tee, but now capacitors have entered the scene and I'm stumped.
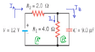
The circuit in the drawing (attached) shows two resistors, a capacitor, and a battery. When the capacitor is fully charged, what is the magnitude q of the charge on one of its plates?
I apologise for the terrible resolution of the image, but I think it's still readable.
From the junction rule;
IA = IB + IC
For loop A;
12V = 2IA + 4IC
My textbook says a loop does not need to contain a battery, so my expression for loop B is;
4Ic = Q/C
I am confused about whether the capacitor represents a voltage drop, because to me, it seems like a fully charged capacitor should create a potential rise.
I am unsure about whether I need to make an expression for the loop created by the 'outer' sides of the circuit.
Please can you help me in this regard?
Thanks.
I thought I had questions concerning Kirchoff's rules down to a tee, but now capacitors have entered the scene and I'm stumped.
Homework Statement
The circuit in the drawing (attached) shows two resistors, a capacitor, and a battery. When the capacitor is fully charged, what is the magnitude q of the charge on one of its plates?
Homework Equations
The Attempt at a Solution
I apologise for the terrible resolution of the image, but I think it's still readable.
From the junction rule;
IA = IB + IC
For loop A;
12V = 2IA + 4IC
My textbook says a loop does not need to contain a battery, so my expression for loop B is;
4Ic = Q/C
I am confused about whether the capacitor represents a voltage drop, because to me, it seems like a fully charged capacitor should create a potential rise.
I am unsure about whether I need to make an expression for the loop created by the 'outer' sides of the circuit.
Please can you help me in this regard?
Thanks.