A way to sort of see the connection between quantum field theory and quantum mechanics is (and
@Demystifier has a lot to say about this) to look at how a QFT can arise from many-particle quantum mechanics.
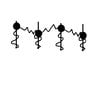
Here's a toy problem that is similar to real solid state physics problems. Imagine that you have a lattice of atoms that are fixed in place in the x-direction, but are free to move in the y-direction. I'm going to model the forces on the atoms using harmonic oscillators. Each atom is connected to its base with a spring, that will tend to keep it in place vertically. In addition, there is a second spring connecting each atom to its nearest neighbor. For simplicity of the calculation, let me assume that the equilibrium length of the horizontal springs is negligible.
We can write down a classical (nonquantum, nonrelativistic) lagrangian for the collection of atoms:
##L = \sum_j \frac{1}{2} m (\dot{y_j})^2 - \frac{k_1}{2} (y_j)^2 - \frac{k_2}{2} (y_{j+1} - y_j)^2##
where ##m## is the mass of an atom, and ##y_j## is the vertical position of atom number ##j## and ##k_1## and ##k_2## are two spring constants, and where ##\dot{A}## means ##\frac{dA}{dt}##.
If the number of atoms is very large, and the energies of the atoms are smallish, then we can approximate the discrete lattice by a continuous function ##\phi(x)##:
##y_j = K \phi(j \Delta x)## where ##\Delta x## is the horizontal distance between atoms. (##K## is a scaling factor to be determined later)
##\dot{y_j} = K \dot{\phi}##
##y_{j+1} - y_j \approx K \Delta x \phi'## (where ##'## means a derivative with respect to ##x##).
In terms of ##\phi##, the lagrangian becomes:
##L = \sum_j \Delta x [\frac{mK^2}{2 \Delta x} (\dot{\phi})^2 - \frac{k_1 K^2}{2 \Delta x} \phi^2 - \frac{k_2 K^2 \Delta x}{2} (\phi')^2]## (I've factored out ##\Delta x## in anticipation of approximating the sum by an integral).
Now, let's choose our scaling factor ##K## so that ##\frac{mK^2}{ \Delta x} = 1##. Then let's define new constants:
##\mu^2 = \frac{k_1 K^2}{\Delta x}##
##\bar{c}^2 = k_2 K^2 \Delta x ##
In terms of these constants,
##L = \sum_j \Delta x [\frac{1}{2} (\dot{\phi})^2 - \frac{\mu^2}{2} \phi^2 - \bar{c}^2 (\phi')^2]##
##\approx \int dx [\frac{1}{2} (\dot{\phi})^2 - \frac{\mu^2}{2} \phi^2 - \bar{c}^2 (\phi')^2]##
This is exactly the lagrangian for a relativistic neutral spin-zero quantum field in one spatial dimension, (if you interpret ##\bar{c}## as the speed of light).
So the classical (nonrelativistic, nonquantum) theory of the toy lattice problem transforms, in the continuum limit to what looks like a relativistic (nonquantum) field theory.
Now, to make the description quantum-mechanical, we can go back to the original problem, and interpret the ##y_j## and ##\dot{y_j}## as operators, instead of numbers. We can transform from the lagrangian form to the hamiltonian form by introducing a momentum ##p_j## defined by:
##p_j = \frac{\partial \mathcal{L}}{\partial \dot{y_j}} = m \dot{y_j}##
Then we introduce the commutation relation: ##[p_j, y_k] = -i \delta_{jk}##. This gives rise to the equivalent commutation relation for ##\phi##:
##[\dot{\phi}(x), \phi(x')] = -i \delta(x-x')##
So this reinterpretation of the many-particle quantum mechanical problem as a quantum field-theory problem illustrates some facts about ##\phi##. It is
not a wave function. Going back to the original problem, you can see that ##\phi## is the amplitude for the
classical displacement of the atoms in the lattice. The quantum mechanics does not come in by interpreting ##\phi^2## as a probability. It isn't a probability. Instead, for each atom, there would be a corresponding wave function ##\psi_j(y)## giving the probability amplitude that atom number j has vertical displacement ##y##. When you shift to the field-theoretic interpretation, there would correspondingly be a wave function giving the probability amplitude that the classical wave ##\phi## has a particular value at a particular point.