diewolke
- 2
- 0
Hello physicsforums community.
I have recently learned about Lagrange multipliers and have been given three problems to solve. Could you guys please go over my work and see if I have the gist of it? One question, a theoretical one, I have no idea how to begin. Any advice regarding this would be welcomed.
Thanks
PS: Please excuse any formatting errors; this is my first post on this forum.
--------------
Question 1a
f:R^2-->R^2, (x,y)-->x^2-y^2, and let S be the circle of radius 1 around the origin.
In two dimensions, the condition that
\nablaf(x,y,z)=\lambda\nablag(x,y,z) at x_{o}, that is, \nablaf(x,y,z) and \nablag(x,y,z) are parallel at x_{o}[/tex] is the same as the level curves being tangent at x_{.}. Give the reason why you may conclude that the level curves are tangent at x_{o}.
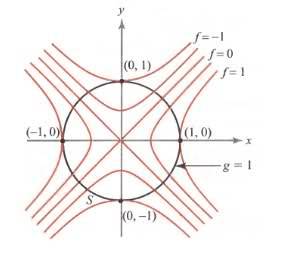
2. f:R^2-->R^2, (x,y)-->x^2-y^2 and
g:R^2-->R^1, (x,y)--> x^2+y^2 (obtained from the statement about S)
3. I simply do not have a clue how to go about this. I know that the gradient of a function is given by the coordinates which are the function's partial derivatives. I also know that the gradient points to the direction of highest increase for a function at a particular point. Regarding level sets, I know that level sets are given by all (x,..x_{n}) such that f(x,..,x_{n})=c, where c is a constant. I am not sure how to utilize this information to produce an answer. Any advice?
---------------
Question 1b
1. Using the Lagrange multiplier method, maximize the function f(x,y,z)=x+z subject to the constraint x^2+y^2+z^2=51
2. \nablaf(x,y,z)=\lambda\nablag(x,y,z)
3.
Having computed the gradients for g and f, listed the partials separately, and using the above equation, I obtained the following system of equations:
1=2x\lambda
0=2y\lambda
1=2z\lambda
Solving for x, y, and z, I obtained
x=1/(2lambda)
y=0 and
z=x=1/(2lambda)
and here is the constraint once more: x^2+y^2+z^2=51
substituting the values of x, y, and z into the above expression,
I get \lambda=+ or - \frac{1}{\sqrt{102}}
using this value to solve for x, y, and z, I get that
x=+ or -\frac{\sqrt{102}}{2}
y=0 and
z=+ or -\frac{\sqrt{102}}{2}
plugging in these values into f(x,y,z)=x+z,
I find that the max must be \sqrt{102}. Is this correct?
----------
I will post the third question shortly.
Thank you again
I have recently learned about Lagrange multipliers and have been given three problems to solve. Could you guys please go over my work and see if I have the gist of it? One question, a theoretical one, I have no idea how to begin. Any advice regarding this would be welcomed.
Thanks
PS: Please excuse any formatting errors; this is my first post on this forum.
--------------
Question 1a
f:R^2-->R^2, (x,y)-->x^2-y^2, and let S be the circle of radius 1 around the origin.
In two dimensions, the condition that
\nablaf(x,y,z)=\lambda\nablag(x,y,z) at x_{o}, that is, \nablaf(x,y,z) and \nablag(x,y,z) are parallel at x_{o}[/tex] is the same as the level curves being tangent at x_{.}. Give the reason why you may conclude that the level curves are tangent at x_{o}.
2. f:R^2-->R^2, (x,y)-->x^2-y^2 and
g:R^2-->R^1, (x,y)--> x^2+y^2 (obtained from the statement about S)
3. I simply do not have a clue how to go about this. I know that the gradient of a function is given by the coordinates which are the function's partial derivatives. I also know that the gradient points to the direction of highest increase for a function at a particular point. Regarding level sets, I know that level sets are given by all (x,..x_{n}) such that f(x,..,x_{n})=c, where c is a constant. I am not sure how to utilize this information to produce an answer. Any advice?
---------------
Question 1b
1. Using the Lagrange multiplier method, maximize the function f(x,y,z)=x+z subject to the constraint x^2+y^2+z^2=51
2. \nablaf(x,y,z)=\lambda\nablag(x,y,z)
3.
Having computed the gradients for g and f, listed the partials separately, and using the above equation, I obtained the following system of equations:
1=2x\lambda
0=2y\lambda
1=2z\lambda
Solving for x, y, and z, I obtained
x=1/(2lambda)
y=0 and
z=x=1/(2lambda)
and here is the constraint once more: x^2+y^2+z^2=51
substituting the values of x, y, and z into the above expression,
I get \lambda=+ or - \frac{1}{\sqrt{102}}
using this value to solve for x, y, and z, I get that
x=+ or -\frac{\sqrt{102}}{2}
y=0 and
z=+ or -\frac{\sqrt{102}}{2}
plugging in these values into f(x,y,z)=x+z,
I find that the max must be \sqrt{102}. Is this correct?
----------
I will post the third question shortly.
Thank you again