Boltzman Oscillation
- 233
- 26
Given the figure, how can i arrive to this formula knowing that angular momentum is conserved?
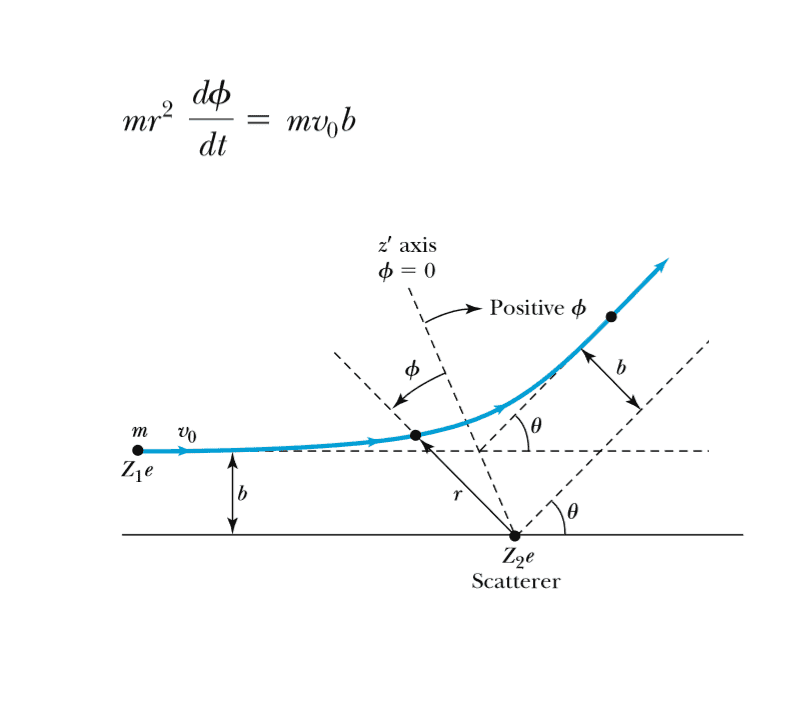
I know that p = mv and L = p x r. So the initial momentum will be L1 = mV x R and the final momentum will be L2 = mv x r.
I am not sure how R will equal to b since the distance between the initial position of the electron is clearly not b distance apart from the scatterer. I am also not sure how to modify the final angular momentum to fit the formula.
I know that p = mv and L = p x r. So the initial momentum will be L1 = mV x R and the final momentum will be L2 = mv x r.
I am not sure how R will equal to b since the distance between the initial position of the electron is clearly not b distance apart from the scatterer. I am also not sure how to modify the final angular momentum to fit the formula.
