gabrielh
- 79
- 0
Homework Statement
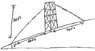
A 100-foot vertical tower is to be erected on the side of a hill that makes a 6^{\circ} angle with the horizontal. Find the length of each of the two guy wires that will be anchored 65 feet uphill and downhill from the base of the tower.
Homework Equations
Law of Cosines
a^{2} = b^{2} + c^{2} - (2bc)cos(a)
b^{2} = a^{2} + c^{2} - (2ac)cos(b)
c^{2} = a^{2} + b^{2} - (2ab)cos(c)
I included an sketched version of the image that was provided with this problem. Please forgive the sub par drawing skills.
The Attempt at a Solution
With a bit of help getting started and finding a couple of the unknown angles, I should be able to work this problem easily. I understand law of cosines quite well, I'm just unsure of the best way to begin this problem.