- #1
spaceman231
- 4
- 0
Lenz law problem wire and expanding loop
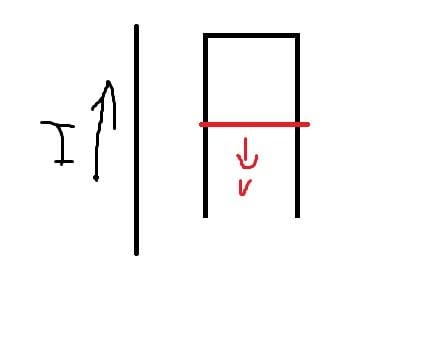
The loop has current radius R the red bar moves at velocity V. The distance the wire is from the loop is d and the top of the loop is length l Find the induced emf and the direction of the current in the loop.
\Phi_{B}=\oint\textit{B} \bullet\textit{dA}
ε=-\frac{d\Phi_{B}}{dt}=\oint\vec{E}\bulletd\vec{l}
The wire causes a b field into the page inside the loop and v moving down means the flux is getting larger so the induced current will be counter clockwise to make a b field going out of the page to counter the expanding area.
I know that the b field from the left part of the loop to the right decreases.
I am trying to find out which way to integrate for flux because if the bar was not moving down flux would need to be integrated like this
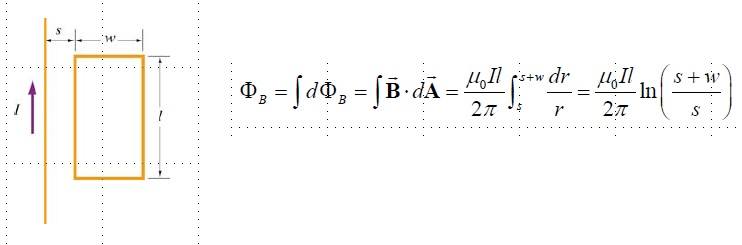since the b field from the left part of the loop to the right decreases cause it's distance is increasing from the wire creating the b field.
But since the bar is moving down how would you integrate to calculate flux?
Homework Statement
The loop has current radius R the red bar moves at velocity V. The distance the wire is from the loop is d and the top of the loop is length l Find the induced emf and the direction of the current in the loop.
Homework Equations
\Phi_{B}=\oint\textit{B} \bullet\textit{dA}
ε=-\frac{d\Phi_{B}}{dt}=\oint\vec{E}\bulletd\vec{l}
The Attempt at a Solution
The wire causes a b field into the page inside the loop and v moving down means the flux is getting larger so the induced current will be counter clockwise to make a b field going out of the page to counter the expanding area.
I know that the b field from the left part of the loop to the right decreases.
I am trying to find out which way to integrate for flux because if the bar was not moving down flux would need to be integrated like this
But since the bar is moving down how would you integrate to calculate flux?
Last edited:
