Jack_O
- 64
- 0
Hi all, I'm new to the forums so if i do something stupid don't hesitate to tell me.
Anyway I'm struggling with this problem:

I could do part a ok, but part b has me stumped, I am in the second year of a physics degree and this is a from a maths problem sheet, i haven't done line integrals before now and they have me a bit confused, my textbook has a few examples but none of them include vectors and http://en.wikipedia.org/wiki/Line_integral" has me even more confused.
Here is my attempt so far:
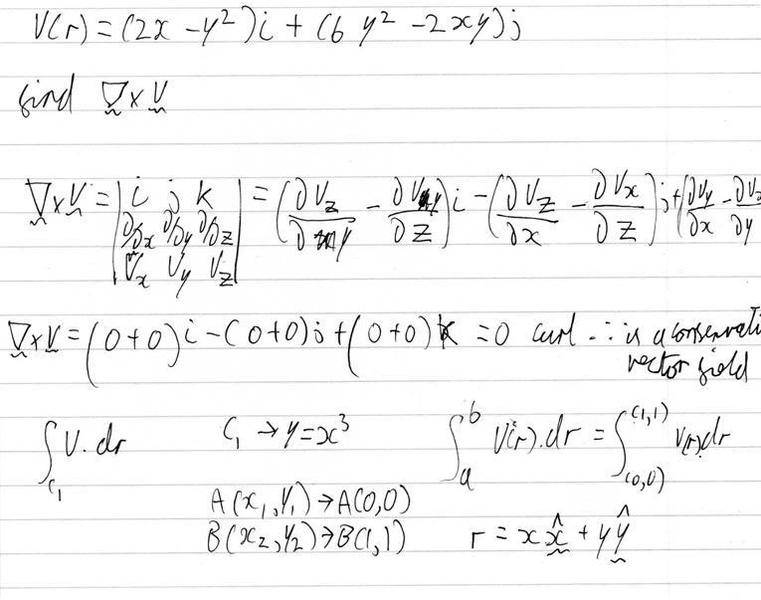
(please excuse bad handwriting, i am dyslexic)
I basically don't know where to begin with it, any help much appreciated.
Anyway I'm struggling with this problem:
I could do part a ok, but part b has me stumped, I am in the second year of a physics degree and this is a from a maths problem sheet, i haven't done line integrals before now and they have me a bit confused, my textbook has a few examples but none of them include vectors and http://en.wikipedia.org/wiki/Line_integral" has me even more confused.
Here is my attempt so far:
(please excuse bad handwriting, i am dyslexic)
I basically don't know where to begin with it, any help much appreciated.
Last edited by a moderator: