y.moghadamnia
- 23
- 1
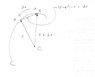
in line integrals we always need a vector element of distance. I can't understand the difference between ds and dr. is ds for all kinds of paths (even curly ones) and dr only for straight lines, or theyre the same? I am confused, or maybe dr is just the magnitude of ds, and the vector here is the ds,which one is true?