zenterix
- 774
- 84
- Homework Statement
- Consider the circuit containing the nonlinear element ##N## as shown below in Figure 3.
The ##i-v## relation fro the element ##N## is
$$i_A=(10\mathrm{A}(1-e^{-v_A/5\mathrm{V}})$$
(a) Write an equation which relates voltage ##V_A## to input voltage ##v_I##.
(b) Solve for voltate ##v_A## when ##v_I=\mathrm{10V}##.
(c) Find the incremental change in ##v_A## for a ##2%## increase in ##v_I## and calculate the ratio ##\Delta v_A/\Delta v_I##.
(d) Find the value for the incremental resistance of the nonlinear element ##N## by linearizing the expression for ##i_A## about the operating point when ##v_I=\mathrm{10V}##.
(e) Draw the incremental circuit model for the circuit shown in Figure 3.
(f) Find the ratio ##\Delta v_A/\Delta v_I## from the incremental circuit model and compare it with your exact model from part (c).
- Relevant Equations
- ##v=iR##
I think I managed to solve the entire problem, as I show below. My main doubt is about item (e), the incremental circuit.
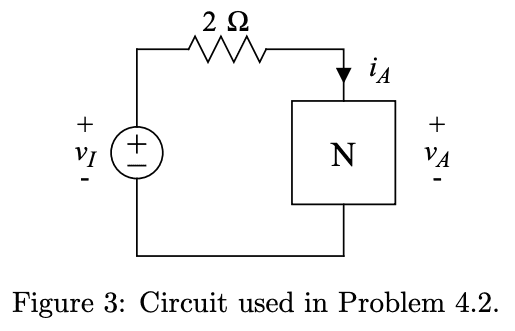
Part (a)
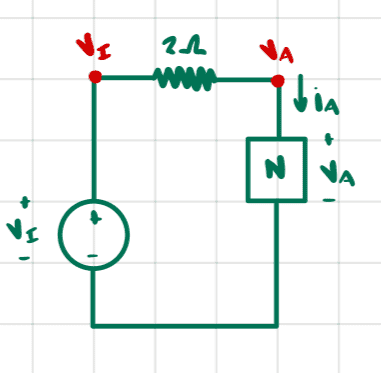
Using the node method and KCL we reach
$$\frac{v_I-v_A}{2}=10(1-e^{-v_A/5})\tag{1}$$
Part (b)
We can simplify (1) to
$$v_A=5\ln{\left ( \frac{20}{v_A+20-v_I} \right )}\tag{2}$$
If we sub in ##v_I=\mathrm{10V}## and use Newton-Raphson we find that ##v_A=\mathrm{2.39V}##.
Part (c)
Now let ##v_I=\mathrm{10.20V}##. Again by Newton-Raphson we find that ##v_A=\mathrm{2.45V}##.
Thus, ##\frac{\Delta v_A}{\Delta v_I}=\frac{0.06}{0.2}=0.3##.
Part (d)
Given ##i_A=10(1-e^{v_A/5})##, linearization about ##v_A=2.39\mathrm{V}## gives us
$$\Delta i_A=2e^{-2.39/5}\Delta v_A\tag{3}$$
Note that this means that the incremental resistance of the nonlinear element is ##\frac{1}{2e^{-2.39/5}}##.
Part (e)
I think the circuit is
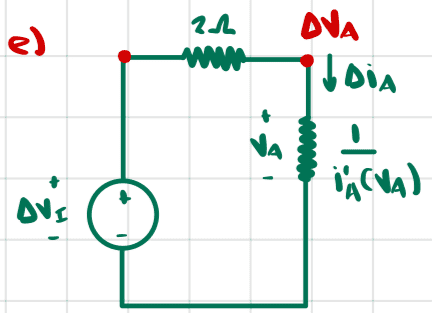
Part (f)
Using the node method and our linearized expression for ##\Delta i_A## we have
$$\frac{\Delta v_I-\Delta v_A}{2}=2e^{-2.39/5}\Delta v_A\tag{4}$$
For ##\Delta v_I=0.2## and solving for ##\Delta v_A## we get ##\Delta v_A=0.0574##.
Thus, ##\frac{\Delta v_A}{\Delta v_I}=\frac{0.0574}{0.2}\approx 0.287##.
We compare this with the value we found in (c) which was 0.3.
Part (a)
Using the node method and KCL we reach
$$\frac{v_I-v_A}{2}=10(1-e^{-v_A/5})\tag{1}$$
Part (b)
We can simplify (1) to
$$v_A=5\ln{\left ( \frac{20}{v_A+20-v_I} \right )}\tag{2}$$
If we sub in ##v_I=\mathrm{10V}## and use Newton-Raphson we find that ##v_A=\mathrm{2.39V}##.
Part (c)
Now let ##v_I=\mathrm{10.20V}##. Again by Newton-Raphson we find that ##v_A=\mathrm{2.45V}##.
Thus, ##\frac{\Delta v_A}{\Delta v_I}=\frac{0.06}{0.2}=0.3##.
Part (d)
Given ##i_A=10(1-e^{v_A/5})##, linearization about ##v_A=2.39\mathrm{V}## gives us
$$\Delta i_A=2e^{-2.39/5}\Delta v_A\tag{3}$$
Note that this means that the incremental resistance of the nonlinear element is ##\frac{1}{2e^{-2.39/5}}##.
Part (e)
I think the circuit is
Part (f)
Using the node method and our linearized expression for ##\Delta i_A## we have
$$\frac{\Delta v_I-\Delta v_A}{2}=2e^{-2.39/5}\Delta v_A\tag{4}$$
For ##\Delta v_I=0.2## and solving for ##\Delta v_A## we get ##\Delta v_A=0.0574##.
Thus, ##\frac{\Delta v_A}{\Delta v_I}=\frac{0.0574}{0.2}\approx 0.287##.
We compare this with the value we found in (c) which was 0.3.