- #1
kostoglotov
- 234
- 6
In HS they just taught you the formula for it (the cofactor method) and a few other things, such as det(A) = 0 means A is singular.
I finally reached Ch 5 of MIT OCW Intro to Linear Algebra, and I was really hoping that seeing how determinants are derived from first principles would give me some insight into what the determinant means...aside from whether or not the matrix is singular. I can follow the derivation, through the Big Formula, using the first three properties (det(I) = 1, row swap multiplies by -1, and linearity of determinants).
I have seen how the [itex]A \times adj(A) = det(A)\times I[/itex]
I have shown myself how the determinant for a 2x2 and 3x3 matrix arises purely from elimination, and considering the case if the last pivot is zero.
Ie:
[tex]\begin{bmatrix}a & b\\ 0 & d-\frac{bc}{a}\end{bmatrix}[/tex]
and
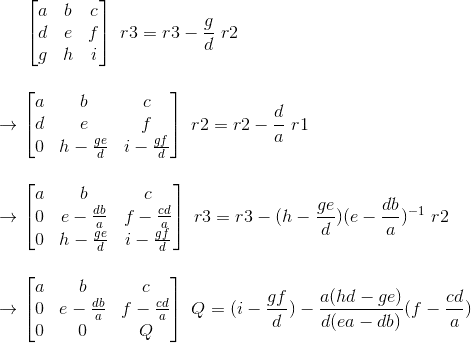
imgur link: http://i.imgur.com/BDjXWcn.gif
What I've learned now just begs a further question, rather than, "why is the determinant important/ what does the determinant means?", I am now wondering, "what do the pivots, and the product of the pivots mean?" Aside of course from indicating whether or not the matrix is singular.
I finally reached Ch 5 of MIT OCW Intro to Linear Algebra, and I was really hoping that seeing how determinants are derived from first principles would give me some insight into what the determinant means...aside from whether or not the matrix is singular. I can follow the derivation, through the Big Formula, using the first three properties (det(I) = 1, row swap multiplies by -1, and linearity of determinants).
I have seen how the [itex]A \times adj(A) = det(A)\times I[/itex]
I have shown myself how the determinant for a 2x2 and 3x3 matrix arises purely from elimination, and considering the case if the last pivot is zero.
Ie:
[tex]\begin{bmatrix}a & b\\ 0 & d-\frac{bc}{a}\end{bmatrix}[/tex]
and
imgur link: http://i.imgur.com/BDjXWcn.gif
What I've learned now just begs a further question, rather than, "why is the determinant important/ what does the determinant means?", I am now wondering, "what do the pivots, and the product of the pivots mean?" Aside of course from indicating whether or not the matrix is singular.