- #1
Saitama
- 4,243
- 93
Homework Statement
Homework Equations
The Attempt at a Solution
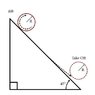
The force on the loop due to magnetic field in the direction normal to the incline is ##qvB##.
Balancing forces in the direction normal to the incline,
[tex]mg\cos\alpha=qvB+N[/tex]
where ##N## is the normal reaction due to incline and v is the velocity of CM of loop.
When the loop takes off, N=0 i.e
[tex]mg\cos\alpha=qvB[/tex]
Also, ##v=g\sin\alpha t##. Substituting this in the above expression and solving for t, I get ##t=1 sec## but this is wrong.