Magnetic Field, copper wire, and solenoid problem.

AI Thread Summary
To solve the magnetic field problem involving a solenoid made from a 20.0 m long copper wire, it's essential to determine the number of turns (N) the wire makes around the solenoid and the solenoid's length (L). The wire's diameter, including insulation, is 2.30 mm, and the solenoid's diameter is 2.50 cm. By calculating how many times the wire can wrap around the solenoid's circumference, one can find N. The magnetic field at the center of the solenoid can then be calculated using the appropriate formulas. This approach effectively leads to finding the magnetic field in Teslas when a current of 26.0 A is applied.
Alpha Russ Omega
Messages
30
Reaction score
0
Hello:
I am having trouble starting this problem.

"20.0 m long copper wire, 2.30 mm in diameter including insulation, is tightly wrapped in a single layer with adjacent coils touching, to form a solenoid of diameter 2.50 cm. What is the field at the center when the current in the wire is 26.0 A? Give the field in Teslas."

I figured I would need to use these equations:
a6f1b19204e85bbfab2c63229c0a8f81.png

efb9567caecf0adf95ae08672ab34247.png

3adb9c5743955ba0dc684224ebfff3b2.png

9bd719e1f5ce0a61a8646e08c8a867d0.png


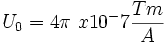
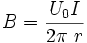
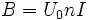
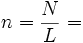
Not sure where to start...

Any help would be greatly appreciated.
 
Last edited by a moderator:
Physics news on Phys.org
The trick here is to determine how many turns (N) the wire makes around the solenoid and how long (L) the solenoid is. So, haow many times can 20 meters wrap around this solenoid's circumference?
 
Thank you for the hint. That helped me solve the problem. :smile:
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Why is magnetic field half at the sides of a solenoid?
Replies
11
Views
3K
Current in circular wire surrounding infinite solenoid in a circuit
Replies
7
Views
1K
EE: How to heat a magnet with a wire while levitating a superconductor?
Replies
14
Views
2K
Change in the Electric Field Due to a Copper Wire Being Inserted
Replies
14
Views
5K
Solenoid with current carrying wire inside
Replies
3
Views
3K
Square copper wire loop within a magnetic field
Replies
3
Views
2K
Verify Magnetic Induction Homework: 50A Copper Wire 0.5*10-2m
Replies
5
Views
2K
Magnetic field outside the solenoid
Replies
21
Views
5K
Strength of magnetic field at the end of a wire wrapped nail.
Replies
1
Views
1K
{ help } Calculating the B-field at the center of a solenoid
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top