FelixTheWhale
- 4
- 0
Hello friends, I am trying to find how calculate the magnetic field created by current loop considering that there is a some geometry of material that can enhance the magnetic field. I thought it can be solved by multipling by permeability μ but realized that the iron core changes the picture of magnetic qualitatively.
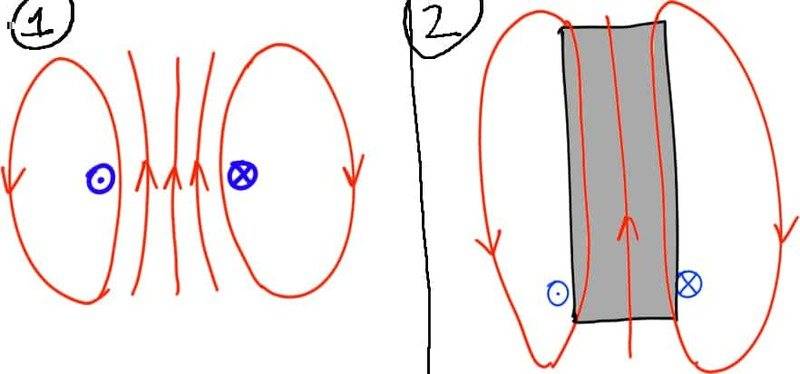
To illustrate this i attached image for: only coil (1) and coil around the iron bar (2).
For the first picture, it is easy to integrate by Bio-Savart-Laplace law, but..
How to find he field for any point at the second picture?
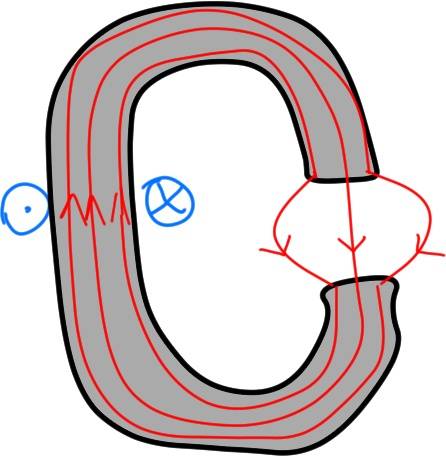
Or, more complicated case:
To illustrate this i attached image for: only coil (1) and coil around the iron bar (2).
For the first picture, it is easy to integrate by Bio-Savart-Laplace law, but..
How to find he field for any point at the second picture?
Or, more complicated case:
Last edited: