*Alice*
- 26
- 0
Dear all,
would anyone be able to help me with the following problem
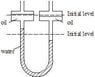
In the manometer shown in the figure, the reservoir diameters are 50 mm and the tube diameters are 10 mm. The upper fluid is an oil of density 850 kg/m3, and the lower fluid (hatched) is water. Initially the levels of oil in the two reservoirs are the same, and the levels of water in the two tubes are the same. If a pressure differential of 200 Pa is applied to the air above the oil in the reservoirs, what is then the difference in water levels?
PICTURE SEE ATTACHED FILE
Basically, I tried to calculate the change in height on the top rhs and then calculated the height difference at the water on the right hand side since the relation
h1 = h2 (d/D)^2
holds. due to the symmetry h on the lhs should be the same and hence dh=2h
which gives me the wrong result.
Can anyone please give me a hint? THat would be amazing! Thanks a lot!
would anyone be able to help me with the following problem
In the manometer shown in the figure, the reservoir diameters are 50 mm and the tube diameters are 10 mm. The upper fluid is an oil of density 850 kg/m3, and the lower fluid (hatched) is water. Initially the levels of oil in the two reservoirs are the same, and the levels of water in the two tubes are the same. If a pressure differential of 200 Pa is applied to the air above the oil in the reservoirs, what is then the difference in water levels?
PICTURE SEE ATTACHED FILE
Basically, I tried to calculate the change in height on the top rhs and then calculated the height difference at the water on the right hand side since the relation
h1 = h2 (d/D)^2
holds. due to the symmetry h on the lhs should be the same and hence dh=2h
which gives me the wrong result.
Can anyone please give me a hint? THat would be amazing! Thanks a lot!