emadbeni
- 7
- 0
Hello guys,
actually I'am working on a model to describe the creep-behaviour of a concrete specimen. This model is based on a 'generalized maxwell-chain'. I attached a picture, where you can see it:
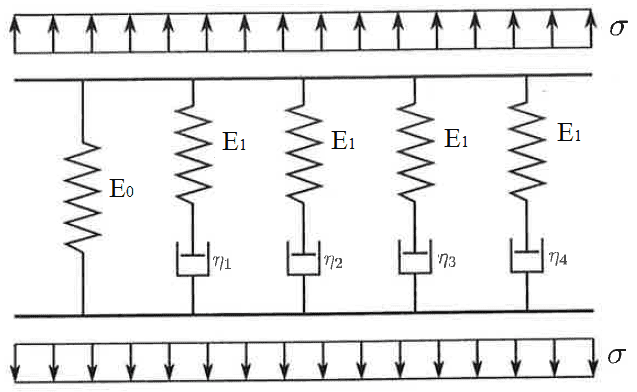
The acting load is the tension \sigma, while E_0 and E_1 are the stiffnesses of the Hooke-springs and \eta_i are the viscosities of the Newton-dashpots.
All these parameters are "hidden" in the parameters a_i, b_i of the constitutive equation which describes the behaviour of this model by:
b_0\cdot\epsilon+b_1\cdot\dot\epsilon+b_2\cdot\ddot\epsilon+b_3\cdot\dddot\epsilon + b_4\cdot\ddddot\epsilon = a_0\cdot\sigma +a_1\cdot\dot\sigma + a_2\cdot\ddot\sigma + a_3\cdot\dddot\sigma + a_4\cdot\ddddot\sigma
To simplify the whole problem, I assume that these parameters a_i, b_i won't change within time.
Now I want to test the material by performing a "simple" creep-test. This means that at a time t, a tension \sigma > 0 is applied and stays constant:
t = 0: σ = 0
t = 1: σ = 0
t = 2: σ = 0
t = 3: σ = 0
t = 3,001: σ = 1
t = 4: σ = 1
t = 5: σ = 1
t = 6: σ = 1
t = 7: σ = 1
(etc.)
If I want to know the resulting strain \epsilon at the end of a time-step t-t0, i can solve the given equation which actually can be simplified to (because the \sigma is constant in a time-step, all of it's derivatives are zero):
b_0\cdot\epsilon+b_1\cdot\dot\epsilon+b_2\cdot\ddot\epsilon+b_3\cdot\dddot\epsilon + b_4\cdot\ddddot\epsilon = a_0\cdot\sigma
This is a fourth-order ODE with constant coefficients that can be solved analytically. In a time-step based calculation, I have to solve the equation for each time-step by the formulation of correct initial conditions. ... and there is the problem:
If I want to get the strain et the end of the time step (t = 3,001) - (t_0 = 3) I mean that the initial conditions for the \epsilon, \dot\epsilon, ... are:
\epsilon(t = 3) = 0 + \frac{\Delta\sigma(t-t_0)}{E_0 + 4\cdot E_1} (at the begin \epsilon is zero, but there's always a kind of elastic deformation, when some stress is applied)
\dot\epsilon(t = 3) = \frac{\frac{\Delta\sigma}{t - t_0}}{E_0 + 4\cdot E_1} (this is the velocity of the elastic strain)
\ddot\epsilon(t = 3) = 0 (I guess ... but I am not sure)
\dddot\epsilon(t = 3) = 0 (same here ...)
So far so good. If I come to the next time step (t = 4) - (t_0 = 3,001), I have to solve the equation again. Now with different initial conditions:
\epsilon(t = 4) = \epsilon(t = 3,001)+ \frac{\Delta\sigma(t-t_0) = 0}{E_0 + 4\cdot E_1}
\dot\epsilon(t = 4) = ... I don't know what... (I don't think that it is \dot\epsilon(t = 3,001) and I also doubt that it is zero ...)
\ddot\epsilon(t = 4) = ... (same here ...)
\dddot\epsilon(t = 4) = ... (same here ...)
I hope I described the problem good enough that someone can help me ... this would be great!
Thank you in advance
actually I'am working on a model to describe the creep-behaviour of a concrete specimen. This model is based on a 'generalized maxwell-chain'. I attached a picture, where you can see it:
The acting load is the tension \sigma, while E_0 and E_1 are the stiffnesses of the Hooke-springs and \eta_i are the viscosities of the Newton-dashpots.
All these parameters are "hidden" in the parameters a_i, b_i of the constitutive equation which describes the behaviour of this model by:
b_0\cdot\epsilon+b_1\cdot\dot\epsilon+b_2\cdot\ddot\epsilon+b_3\cdot\dddot\epsilon + b_4\cdot\ddddot\epsilon = a_0\cdot\sigma +a_1\cdot\dot\sigma + a_2\cdot\ddot\sigma + a_3\cdot\dddot\sigma + a_4\cdot\ddddot\sigma
To simplify the whole problem, I assume that these parameters a_i, b_i won't change within time.
Now I want to test the material by performing a "simple" creep-test. This means that at a time t, a tension \sigma > 0 is applied and stays constant:
t = 0: σ = 0
t = 1: σ = 0
t = 2: σ = 0
t = 3: σ = 0
t = 3,001: σ = 1
t = 4: σ = 1
t = 5: σ = 1
t = 6: σ = 1
t = 7: σ = 1
(etc.)
If I want to know the resulting strain \epsilon at the end of a time-step t-t0, i can solve the given equation which actually can be simplified to (because the \sigma is constant in a time-step, all of it's derivatives are zero):
b_0\cdot\epsilon+b_1\cdot\dot\epsilon+b_2\cdot\ddot\epsilon+b_3\cdot\dddot\epsilon + b_4\cdot\ddddot\epsilon = a_0\cdot\sigma
This is a fourth-order ODE with constant coefficients that can be solved analytically. In a time-step based calculation, I have to solve the equation for each time-step by the formulation of correct initial conditions. ... and there is the problem:
If I want to get the strain et the end of the time step (t = 3,001) - (t_0 = 3) I mean that the initial conditions for the \epsilon, \dot\epsilon, ... are:
\epsilon(t = 3) = 0 + \frac{\Delta\sigma(t-t_0)}{E_0 + 4\cdot E_1} (at the begin \epsilon is zero, but there's always a kind of elastic deformation, when some stress is applied)
\dot\epsilon(t = 3) = \frac{\frac{\Delta\sigma}{t - t_0}}{E_0 + 4\cdot E_1} (this is the velocity of the elastic strain)
\ddot\epsilon(t = 3) = 0 (I guess ... but I am not sure)
\dddot\epsilon(t = 3) = 0 (same here ...)
So far so good. If I come to the next time step (t = 4) - (t_0 = 3,001), I have to solve the equation again. Now with different initial conditions:
\epsilon(t = 4) = \epsilon(t = 3,001)+ \frac{\Delta\sigma(t-t_0) = 0}{E_0 + 4\cdot E_1}
\dot\epsilon(t = 4) = ... I don't know what... (I don't think that it is \dot\epsilon(t = 3,001) and I also doubt that it is zero ...)
\ddot\epsilon(t = 4) = ... (same here ...)
\dddot\epsilon(t = 4) = ... (same here ...)
I hope I described the problem good enough that someone can help me ... this would be great!
Thank you in advance