Challenge Math Challenge - August 2020

[fresh_42]

1. (solved by @nuuskur ) Let $K$ be a non-empty compact subset of $\Bbb{C}$. Construct a bounded operator $u: H \to H$ on some Hilbert space $H$ that has spectrum $\sigma(u) =K$. (MQ)

2. Let $f,g:[0,2]\to\mathbb{R}$ be continuous functions such that $f(0)=g(0)=0$ and $f(2)=g(2)=2$. Show that there exist $a,b\in [0,2)\,,a\neq b\,.$ such that $f(a)-f(b)$ and $g(a)-g(b)$ are both integers. (IR)

3. (solved by @nuuskur ) Let $V$ be a normed vector space and $W$ be a closed linear subspace. If $V/W$ is a Banach space for the quotient norm, show that $V$ is a Banach space as well. (MQ)

4. (solved by @nuuskur ) Let $(\Omega, \mathcal{F}, \Bbb{P})$ be a probability space and $X: \Omega \to \Bbb{R}$ be a random variable. If $\Bbb{P}(X \in A) \in \{0,1\}$ for all Borel sets $A$, show that there is a constant $c \in \Bbb{R}$ such that $\Bbb{P}(X= c) = 1$ (i.e. $X$ is constant almost surely). (MQ)

5. Let $X,Y$ be Banach spaces over the field $\mathbb{R}$ or $\mathbb{C}$. By $B_X(\hat x,R)$ we denote the open ball of this space:
$$B_X(\hat x,R)=\{x\in X\mid \|x-\hat x\|_X<R\},$$ and $\overline B_X(\hat x,R)=\{x\in X\mid \|x-\hat x\|_X\le R\}.$
Consider a continuous bilinear function $A:X\times X\to Y$ such that
$$\|A(x_1,x_2)\|_Y\le a\|x_1\|_X\|x_2\|_X,\quad A(x_1,x_2)=A(x_2,x_1).$$
Let $B:X\to Y$ stand for a bounded linear operator onto:
$$\overline B_Y(0,b)\subseteq B(\overline B_X(0,1))$$ with some positive constant $b$. Let $C$ stand for a fixed element of $Y,\quad \|C\|_Y=c$.
Show that
If $D=b^2-4ac\ge 0$ then the equation
$$A(x,x)+Bx+C=0$$ has a solution. (WR)

6. (solved by @nuuskur ) Show that in ZF the Tychonoff theorem (product of compact spaces is compact) implies the axiom of choice. (MQ)

7. (solved by @nuuskur ) Let $f: (X,d_X) \to (Y,d_Y)$ be a map between metric spaces (not necessarily continuous!). Show that $D(f):= \{x \in X\mid f \mathrm{\ is \ not \ continuous \ at \ x}\}$ is a Borel-measurable set of $X$. (MQ)

8. (solved by @benorin , @Fred Wright , and @nuuskur ) Let $F$ be a meromorphic function (holomorphic up to isolated poles) in $\mathbb{C}$ with the following properties:
(1) $F$ is holomorphic (complex differentiable) in the half plane $H(0)=\{z\in \mathbb{C}\, : \,\Re(z)>0\}.$
(2) $zF(z)=F(z+1).$
(3) $F$ is bounded in the strip $\{z\in \mathbb{C}\, : \,1\leq\Re(z)\leq 2\}.$
Show that $F(z)=F(1)\Gamma(z).$ (FR)

9. (solved by @PeroK ) Show that there exists no continuous function $g: \Bbb{C}\setminus \{0\}\to \Bbb{C}$ such that $e^{g(z)} = z$ for all $z\in \Bbb{C}\setminus \{0\}$ (i.e. there is no continuous logarithm on $\Bbb{C}\setminus \{0\})$. (MQ)
(Corrected version, credits go to @PeroK for pointing out and solving the original problem.)

10. (solved by @PeroK ) Show that if $f$ is any continuous real function and $n$ any positive number (FR),
$$
I:=\int_{n^{-1}}^{n} f\left(x+\dfrac{1}{x}\right)\,\dfrac{\log x}{x}\,dx =0.
$$

High Schoolers only11. (solved by @Not anonymous ) Let $a<b<c<d$ be real numbers. Sort $x=ab+cd\, , \,y=bc+ad\, , \,z=ac+bd$ and prove it.

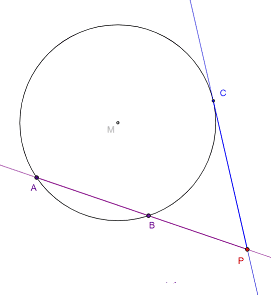
12. (solved by @Not anonymous ) Prove $\overline{CP}^2=\overline{AP}\cdot \overline{BP}\,.$

13. How big is the probability for two pocket aces in Texas Hold'em? Assume we have seen a show down in a heads-up. How many possible combinations are there, how many combinations of possible starting hands can the opponents have? How many possible community cards?

14. (solved by @etotheipi ) Everybody knows that Schrödinger's cat is trapped in the box since $1935.$ Not well known is the fact, that the radioactive material was ten ${}^{14}C$ isotopes. Calculate the probability that the cat is still alive.

15. (solved by @ItsukaKitto ) Show that there is no rational solution for $p^2+q^2+r^2=7.$

 

[etotheipi]

Spoiler: Problem 14

14. Everybody knows that Schrödinger's cat is trapped in the box since $1935.$ Not well known is the fact, that the radioactive material was ten ${}^{14}C$ isotopes. Calculate the probability that the cat is still alive.

The time of an individual decay (which is independent of any other decays) follows an exponential distribution $T \sim \text{Exp}(\lambda)$ with $P(T > t) = e^{-\lambda t}$. The number of atoms out of 10 that have decayed, $X$, follows a binomial distribution $X \sim \text{B}(10, 1-e^{-\lambda t})$, so $$P(X=0) =e^{-10\lambda t}$$The half life of $^{14}\text{C}$ is $t_{1/2} = 5700 \text{ years}$, so $\lambda t = \frac{\ln{2}}{5700 \text{ years}} \times 85 \text{ years} = \frac{17 \ln{2}}{1140}$ which gives, assuming the Geiger counter detects all radiation, $P(X=0) \approx0.90$

But given the maximum lifespan of a cat is only about 16 years...

 

[etotheipi]

Spoiler: Problem 10

10. Show that if $f$ is any continuous real function and $n$ any positive number (FR),
$$
I:=\int_{n^{-1}}^{n} f\left(x+\dfrac{1}{x}\right)\,\dfrac{\log x}{x}\,dx =0.
$$

Let $u = x + \frac{1}{x}$, then $x = \frac{u \pm \sqrt{u^2-4}}{2} := \alpha(u)$ and$$I = \int_{n + n^{-1}}^{n + n^{-1}} f(u) \frac{\log(\alpha(u))}{\alpha(u)(1-\frac{1}{\alpha^2(u)})} du = 0$$because the limits are equal...

Spoiler: Problem 2

2. Let $f,g:[0,2]\to\mathbb{R}$ be continuous functions such that $f(0)=g(0)=0$ and $f(2)=g(2)=2$. Show that there exist $a,b\in [0,2)$ such that $f(a)-f(b)$ and $g(a)-g(b)$ are both integers. (IR)

Doesn't $a = b$ work?

 

[Infrared]

@etotheipi Fair enough, but the intent was to show that it can be done with $a\neq b$.

 

[PeroK]

Spoiler: Problem 10

Let $x = \frac{1}{u}$.
$$I = \int_{n}^{1/n} f(u + \frac 1 u) (-\log(u))u(-\frac{1}{u^2})du = \int_{n}^{1/n} f(u + \frac 1 u) \frac{\log(u)}{u}du = -I$$
Hence $I = 0$

 

[PeroK]

Spoiler: Problem 10

Let $u = x + \frac{1}{x}$, then $x = \frac{u \pm \sqrt{u^2-4}}{2} := \alpha(u)$ and$$I = \int_{n + n^{-1}}^{n + n^{-1}} f(u) \frac{\log(\alpha(u))}{\alpha(u)(1-\frac{1}{\alpha^2(u)})} du = 0$$because the limits are equal...

The new variable $u$ is not on a single interval for $x \in [1/n, n]$.

 

[PeroK]

14. Everybody knows that Schrödinger's cat is trapped in the box since $1935.$ Not well known is the fact, that the radioactive material was ten ${}^{14}C$ isotopes. Calculate the probability that the cat is still alive.

A cat's been trapped in a box for 85 years and you think it might still be alive?

 

[etotheipi]

Spoiler: Problem 9

9. Show that there exists no continuous function $g: \Bbb{C}\setminus \{0\}\to \Bbb{C}$ such that $g(e^{z}) = z$ for all $z\in \Bbb{C}\setminus \{0\}$ (i.e. there is no continuous logarithm on $\Bbb{C}\setminus \{0\})$. (MQ)

This could be ridiculously along the wrong lines, but... let $z = a + bi$, so $$g(e^z) = z$$ $$g(ie^a \sin{b} + e^a \cos{b}) = a + bi$$Since $e^z = ie^a \sin{b} + e^a \cos{b}$, then $\text{Re}(e^z) = e^a \cos{b}$ and $\text{Im}(e^z) = e^a \sin{b}$. This means that $\text{Re}(e^z)^2 + \text{Im}(e^z)^2 = (e^a)^2 (\sin^2 b + \cos^2 b) = (e^a)^2$. We end up with$$a = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}}$$and$$b = \arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi$$So$$g(e^z) = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}} + i \left(\arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi \right)$$but this isn't a function, because it's not possible to recover the specific $n$ that corresponds to $b$?

 

[PeroK]

13. How big is the probability for two pocket aces in Texas Hold'em? Assume we have seen a show down in a heads-up. How many possible combinations are there, how many combinations of possible starting hands can the opponents have? How many possible community cards?

Is there an explanation of this for non-poker-playing high-schoolers?

 

[member 587159]

Spoiler: Problem 9

This could be ridiculously along the wrong lines, but... let $z = a + bi$, so $$g(e^z) = z$$ $$g(ie^a \sin{b} + e^a \cos{b}) = a + bi$$Since $e^z = ie^a \sin{b} + e^a \cos{b}$, then$$a = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}}$$and$$b = \arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi$$so we could say...$$g(z) = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}} + i \left(\arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi \right)$$but this isn't a function, because it's not possible to recover the specific $n$ that corresponds to $b$?

How do you get that expression for the value of $a$?

 

[PeroK]

Spoiler: Problem 9

The complex exponential function is not one-to-one, so cannot have an inverse, continuous or otherwise.

We have: $$e^z = e^x(\cos y + i\sin y)$$
Consider $z_1 = i\frac\pi 2$ and $z_2 = i\frac{5\pi}{2}$, then
$$e^{z_1} = e^{z_2} = i$$

 

[etotheipi]

How do you get that expression for the value of $a$?

I just used that $\text{Re}(e^z) = e^a \cos{b}$ and $\text{Im}(e^z) = e^a \sin{b}$ so $\text{Re}(e^z)^2 + \text{Im}(e^z)^2 = (e^a)^2 (\sin^2 b + \cos^2 b) = (e^a)^2$

 

[member 587159]

Spoiler: Problem 9

The complex exponential function is not one-to-one, so cannot have an inverse, continuous or otherwise.

We have: $$e^z = e^x(\cos y + i\sin y)$$
Consider $z_1 = i\frac\pi 2$ and $z_2 = i\frac{5\pi}{2}$, then
$$e^{z_1} = e^{z_2} = i$$

Your attempt made me realize that I meant to ask for the non-existence of a continuous function $g:\Bbb{C}\setminus \{0\}\to \Bbb{C}$ with $\exp(g(z))=z$ for all $z\in \Bbb{C}\setminus \{0\}$.

Since $\exp: \Bbb{C}\to \Bbb{C}\setminus\{0\}$ is surjective, a set-theoretical right inverse exists but your task is to prove it is not continuous.

Sorry for the inconvenience.
But we are honest and you'll get credit for the attempt but the question remains open.

 

[member 587159]

I just used that $\text{Re}(e^z) = e^a \cos{b}$ and $\text{Im}(e^z) = e^a \sin{b}$ so $\text{Re}(e^z)^2 + \text{Im}(e^z)^2 = (e^a)^2 (\sin^2 b + \cos^2 b) = (e^a)^2$

Add all these details in your attempt so it is easier for me to identify the mistake :) While the question was flawed due to my mistake, I do want to clear out where you were going wrong so we can learn something about it :)

 

[nuuskur]

Compactness is equivalent to finite intersection property (FIP). Cf Proposition 3.1

Spoiler: Problem 6

Let X_\alpha,\ \alpha\in I, be a non-empty family of non-empty sets. We show \prod_{\alpha\in I} X_\alpha \neq\emptyset (AC). Suppose z\notin \bigcup _{\alpha\in I} X_\alpha (the union is a set by ZF). Equip X_\alpha \cup \{z\} with cofinite topology, \alpha\in I. These are compact. By Tikhonov's theorem S:=\prod_{\alpha\in I} X_\alpha\cup\{z\} is compact (under product topology). Fix \alpha\in I. The canonical projection \pi_\alpha :S\to X_\alpha\cup\{z\} is continuous. Since X_\alpha \subset X_\alpha\cup\{z\} is closed (\{z\} is open), the preimage \pi_\alpha^{-1}(X_\alpha) \subseteq S is closed. We show this family of preimages has FIP. Take n\in\mathbb N and let x_{\alpha_j} \in X_{\alpha _j},\ 1\leq j\leq n. We then have
<br /> s(\alpha) := \begin{cases} x_{\alpha _j}, &amp;\text{if }\alpha = \alpha _j \\ z, &amp;\text{otherwise} \end{cases} \Rightarrow s\in \bigcap _{k=1}^n \pi_{\alpha_k}^{-1}(X_{\alpha _k}).<br />
Due to compactness of S there exists y\in S such that y\in \bigcap _{\alpha\in I} \pi _{\alpha}^{-1}(X_\alpha) (because the family of preimages has FIP). By definition \pi _\alpha (y)\in X_\alpha for every \alpha\in I, thus y\in\prod _{\alpha\in I}X_\alpha.

Fun fact. Tikhonov's theorem is equivalent to the axiom of choice.

 

[PeroK]

Your attempt made me realize that I meant to ask for the non-existence of a continuous function $g:\Bbb{C}\setminus \{0\}\to \Bbb{C}$ with $\exp(g(z))=z$ for all $z\in \Bbb{C}\setminus \{0\}$.

Since $\exp: \Bbb{C}\to \Bbb{C}\setminus\{0\}$ is surjective, a set-theoretical right inverse exists but your task is to prove it is not continuous.

Sorry for the inconvenience.
But we are honest and you'll get credit for the attempt but the question remains open.

That's perhaps getting beyond my knowldege. It's not hard to show that the inverse must take the form:
$$g(z) = \ln r + i\theta$$
Which has a discontinuity (branch cut) along the positive x-axis. Is the problem to show that there must be a branch cut somewhere?

 

[etotheipi]

Add all these details in your attempt so it is easier for me to identify the mistake :) While the question was flawed due to my mistake, I do want to clear out where you were going wrong so we can learn something about it :)

Whoops, the last line is supposed to read $g(e^z)$, not $g(z)$. Then I end up with what we'd expect for a logarithm, that $g(z) = \ln{\sqrt{x^2+y^2}} + i\arctan{\frac{y}{x}}$, except I just took a very convoluted route

 

[member 587159]

Spoiler: Problem 9

Suppose we had g:\mathbb C^* \to \mathbb C with g(e^z) = z continuous. It would be a continuous inverse to z\mapsto e^z,\ z\in\mathbb C. Thus \mathbb C\cong \mathbb C^*, but that's impossible. The rough explanation is: homemorphism means same number of holes. \mathbb C^* has a hole in it, so it can't be homemorphic to \mathbb C.

Complex exponential isn't injective, any way, so a contradiction is arrived at earlier, even.

As stated in an earlier post, my question was flawed: see post #13. Sorry for the inconvenience, I'm waiting for post 1 to be edited.

 

[member 587159]

I'm confused. In #13 you asked for a proof that no continuous logarithm exists. Didn't I achieve that?

The question should be $\exp(g(z))=z$ not $g(\exp(z))=z$ as in your attempt.

 

[member 587159]

Compactness is equivalent to finite intersection property (FIP). Cf Proposition 3.1

Spoiler: Problem 6

Let X_\alpha,\ \alpha\in I, be a non-empty family of non-empty sets. We show \prod_{\alpha\in I} X_\alpha \neq\emptyset (AC). Suppose z\notin \bigcup _{\alpha\in I} X_\alpha (the union is a set by ZF). Equip X_\alpha \cup \{z\} with cofinite topology, \alpha\in I. These are compact. By Tikhonov's theorem S:=\prod_{\alpha\in I} X_\alpha\cup\{z\} is compact (under product topology). Fix \alpha\in I. The canonical projection \pi_\alpha :S\to X_\alpha\cup\{z\} is continuous. Since X_\alpha \subset X_\alpha\cup\{z\} is closed (\{z\} is open), the preimage \pi_\alpha^{-1}(X_\alpha) \subseteq S is closed. We show this family of preimages has FIP. Take n\in\mathbb N and let x_{\alpha_j} \in X_{\alpha _j},\ 1\leq j\leq n. We then have
<br /> s(\alpha) := \begin{cases} x_{\alpha _j}, &amp;\text{if }\alpha = \alpha _j \\ z, &amp;\text{otherwise} \end{cases} \Rightarrow s\in \bigcap _{k=1}^n \pi_{\alpha_k}^{-1}(X_{\alpha _k}).<br />
Due to compactness of S there exists y\in S such that y\in \bigcap _{\alpha\in I} \pi _{\alpha}^{-1}(X_\alpha) (because the family of preimages has FIP). By definition \pi _\alpha (y)\in X_\alpha for every \alpha\in I, thus y\in\prod _{\alpha\in I}X_\alpha.

Fun fact. Tikhonov's theorem is equivalent to the axiom of choice.

Looks correct! Well done!

 

[member 587159]

That's perhaps getting beyond my knowldege. It's not hard to show that the inverse must take the form:
$$g(z) = \ln r + i\theta$$
Which has a discontinuity (branch cut) along the positive x-axis. Is the problem to show that there must be a branch cut somewhere?

There are multiple approaches. First, you need to say what convention you use: I guess you write $z=r e^ {i \theta}$. What domain do you allow for $\theta$?

Then, why does $g$ take that form and why does it have a discontinuity?

 

[member 587159]

You're right, I can't read. I'm going to need some black magic for this i.e complex analysis. To be a bit nitpicky, when you say there is no continuous logarithm on \mathbb C^* you actually mean there is no holomorphic map acting as a logarithm, because any logarithm is holomorphic.

Spoiler: Problem 9

Let g: \mathbb C^* \to \mathbb C satisfy the identity e^{g(z)} = z. Then g is holomorphic (Theorem 1.1). Also, @PeroK 's assertion is an immediate corollary (Cor 1.1). On the other hand, g is a logarithm if and only if g is a primitive for \frac{1}{z} such that e^{g(w)} = w for some w\in\mathbb C^*. By Cauchy's integral theorem there cannot exist such a primitive for \frac{1}{z} on \mathbb C^*. Indeed, otherwise we would have
<br /> 0=\oint_{|z|=1} g&#039;(z) dz = \oint_{|z|=1} \frac{1}{z} dz = 2i\pi.<br />

But the plane $\Bbb{C}$ with the origin removed is not simply connected (consider fundamental group), so the theorem does not apply. Also, if the plane was simply connected your theorem would contradict the exercise.

 

[nuuskur]

But the plane $\Bbb{C}$ with the origin removed is not simply connected (consider fundamental group), so the theorem does not apply. Also, if the plane was simply connected your theorem would contradict the exercise.

Correct. My bad.

 

[fresh_42]

Spoiler: Problem 14

The time of an individual decay (which is independent of any other decays) follows an exponential distribution $T \sim \text{Exp}(\lambda)$ with $P(T > t) = e^{-\lambda t}$. The number of atoms out of 10 that have decayed, $X$, follows a binomial distribution $X \sim \text{B}(10, 1-e^{-\lambda t})$, so $$P(X=0) =e^{-10\lambda t}$$The half life of $^{14}\text{C}$ is $t_{1/2} = 5700 \text{ years}$, so $\lambda t = \frac{\ln{2}}{5700 \text{ years}} \times 85 \text{ years} = \frac{17 \ln{2}}{1140}$ which gives, assuming the Geiger counter detects all radiation, $P(X=0) \approx0.90$

But given the maximum lifespan of a cat is only about 16 years...

$5730$ years, but this doesn't affect the answer very much..

 

[member 587159]

Spoiler: Problem 9

This could be ridiculously along the wrong lines, but... let $z = a + bi$, so $$g(e^z) = z$$ $$g(ie^a \sin{b} + e^a \cos{b}) = a + bi$$Since $e^z = ie^a \sin{b} + e^a \cos{b}$, then $\text{Re}(e^z) = e^a \cos{b}$ and $\text{Im}(e^z) = e^a \sin{b}$. This means that $\text{Re}(e^z)^2 + \text{Im}(e^z)^2 = (e^a)^2 (\sin^2 b + \cos^2 b) = (e^a)^2$. We end up with$$a = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}}$$and$$b = \arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi$$So$$g(e^z) = \ln{\sqrt{\text{Re}(e^z)^2 + \text{Im}(e^z)^2}} + i \left(\arctan{\left(\frac{\text{Im}(e^z)}{\text{Re}(e^z)} \right)} + n\pi \right)$$but this isn't a function, because it's not possible to recover the specific $n$ that corresponds to $b$?

Yes, the problem I see with this is that for different choices of $z$ you can have different values of $n$. So you should write $n= n(z)$.

 

[etotheipi]

Assuming that this is correct, is this $g$ continuous?

Well $\text{arctan}$ will throw out a value between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$, so you will have a problem crossing over the negative $x$ axis. If you change $g$ so that the argument is taken between $0$ and $2\pi$, now you have a problem crossing the positive $x$ axis. In any case, I guess not?

 

[member 587159]

Well $\text{arctan}$ will throw out a value between $-\pi$ and $\pi$, so you will have a problem crossing over the negative $x$ axis. If you change $g$ so that the argument is taken between $0$ and $2\pi$, now you have a problem crossing the positive $x$ axis. In any case, I guess not?

Yes, the idea is indeed that on the x-axis trouble arise, but I don't think what you wrote is rigorous enough.

 

[fresh_42]

Spoiler: Problem 10

Let $u = x + \frac{1}{x}$, then $x = \frac{u \pm \sqrt{u^2-4}}{2} := \alpha(u)$ and$$I = \int_{n + n^{-1}}^{n + n^{-1}} f(u) \frac{\log(\alpha(u))}{\alpha(u)(1-\frac{1}{\alpha^2(u)})} du = 0$$because the limits are equal...

Spoiler: Problem 2

Doesn't $a = b$ work?

I have a bit the impression that you tend to ignore the little details, e.g. here when you define two different substitutions and "forget" to manage them. This attitude is o.k. as you concentrate on the core of a problem, and it is wide spread among especially talented students. However, there will be occasions when this becomes a boomerang: exams and publications. This here isn't either, but a playground to practice. Maybe you try to practice being especially correct here. Please don't change your nature, just practice to be pedantic occasionally when it is necessary.

 

[fresh_42]

A cat's been trapped in a box for 85 years and you think it might still be alive?

Well, we cannot know for sure. The cat wasn't specified any further ...

Is there an explanation of this for non-poker-playing high-schoolers?

https://howtoplaypokerinfo.com/poker-101/texas-holdem-rules/

A tiny bit of research can be expected, me thinks. Today more than ever we have to be prepared to consult the internet to look up details.

 

[PeroK]

There are multiple approaches. First, you need to say what convention you use: I guess you write $z=r e^ {i \theta}$. What domain do you allow for $\theta$?

Then, why does $g$ take that form and why does it have a discontinuity?

Okay, it makes sense to look for $e^{g(z)} =z$.

Spoiler: Problem 9

Consider the points on the unit circle, which can be written $z = e^{i\theta} = \cos \theta + i\sin \theta$.

Let $g(z) = \alpha(\theta) + i\beta(\theta)$ with $e^{g(z)} = e^{\alpha}(\cos \beta + i\sin \beta) = z = e^{i\theta}$

We have $\alpha(\theta) = 0$, $\cos \theta = \cos \beta$ and $\sin \theta = \sin \beta$.

If we try to make $\beta$ continuous, then without loss of generality we can take $\beta(0) = 0$, hence $\beta = \theta$ and we get a discontinuity at $\theta = 0$. More generally, for any $\phi$ we could could take $\beta(\phi) = \phi + 2n\pi$ and get the discontinuous branch cut at $\theta = \phi$.

 

[benorin]

Summary:: functional analysis, operator theory, topology, measure theory, calculus
Authors: Math_QED (MQ), Infrared (IR), Wrobel (WR), fresh_42 (FR).

8. Let F be a meromorphic function (holomorphic up to isolated poles) in C with the following properties:
(1) F is holomorphic (complex differentiable) in the half plane H(0)={z∈C:ℜ(z)>0}.
(2) zF(z)=F(z+1).
(3) F is bounded in the strip {z∈C:1≤ℜ(z)≤2}.
Show that F(z)=F(1)Γ(z). (FR)

Spoiler: problem #8

By (3) $\exists M :| F(x+iy) |< M,\forall x\in \left[ 1,2\right]$ and in particular $| F(1) | <M$, also by (2) $F(z)=\tfrac{1}{z} F(z+1)$ and hence F(z) is bounded in the half-plane $H(0)$. Also by (2) $\lim_{z\to 0} F(z)=\lim_{z\to 0}\tfrac{1}{z}F(z+1)=F(1)\lim_{z\to 0}\tfrac{1}{z}=\infty$ but $\lim_{z\to 0}zF(z)=\lim_{z\to 0}F(z+1)=F(1)$ so $z=0$ is a simple pole of $F(z)$ and continuing by (2) we see that $a_k=-k,\forall k\in\mathbb{N}$ are simple poles of $F(z)$.
Define $f(z):=\tfrac{1}{F(z+1)}$ so that $f(z)$ is entire, then by the Weierstrass' Factor Theorem
$$f(z)=f(0)e^{\tfrac{f(0)}{f^\prime (0)}z}\prod_{k=1}^\infty \left\{\left(1-\tfrac{z}{a_k}\right)e^{\tfrac{z}{a_k}}\right\}\quad \text{(eqn 1)}$$

and we have from the definition of $f(z)$ that $f(0)=\tfrac{1}{F(1)}$ and that $f^\prime (0) =-\tfrac{1}{\left[ F^\prime (1)\right] ^2}$ substituting all known values into (eqn 1) we get

$$\tfrac{1}{zF(z)}=\tfrac{1}{F(z+1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}$$

multiply by $z$ on both sides

$$\tfrac{1}{F(z)}=\tfrac{z}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}\quad (eqn 2)$$

set $z=1$ in the above

$$\tfrac{1}{F(1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}}\prod_{k=1}^\infty \left\{\left(1+\tfrac{1}{k}\right)e^{-\tfrac{1}{k}}\right\}$$

do some algebra to get

$$\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}=\lim_{N\to\infty}\sum_{k=1}^N\left[\log \left(1+\tfrac{1}{k}\right)-\tfrac{1}{k}\right]=-\gamma$$

by the definition of Euler's constant $\gamma$, substitute this into (eqn 2) and compare to the Weierstrass product definition of the Gamma function and we have arrived at the required result.

Edit: See below for my next post for a more well explained proof.

 

[nuuskur]

Oh brother, this simply connected business for \mathbb C^* is simply not necessary. Let's go again.

Spoiler: Problem 9

Suppose g:\mathbb C^* \to \mathbb C is continuous with e^{g(z)} \equiv z. Then g is holomorphic, because the exponential map is holomorphic and
<br /> \lim _{z\to z_0} \frac{g(z) - g(z_0)}{z-z_0} = \lim _{g(z)\to g(z_0)} \frac{g(z)-g(z_0)}{e^{g(z)} - e^{g(z_0)}}.<br />
By differentiating we get 1 = g&#039;(z) e^{g(z)} = zg&#039;(z), which implies g&#039;(z) = \frac{1}{z} on \mathbb C^*. But now by Cauchy's integral theorem, we get
<br /> 0 = \oint _{|z|=1} g&#039;(z) dz = \oint_{|z|=1} \frac{1}{z} dz = 2i\pi.<br />
Thus, such a g cannot exist.

Maybe I'm hunting a fly with a 50 cal rifle with armor-piercing rounds..

 

[fresh_42]

Spoiler: problem #8

By (3) $\exists M :| F(x+iy) |< M,\forall x\in \left[ 1,2\right]$ and in particular $| F(1) | <M$, also by (2) $F(z)=\tfrac{1}{z} F(z+1)$ and hence F(z) is bounded in the half-plane $H(0)$. Also by (2) $\lim_{z\to 0} F(z)=\lim_{z\to 0}\tfrac{1}{z}F(z+1)=F(1)\lim_{z\to 0}\tfrac{1}{z}=\infty$ but $\lim_{z\to 0}zF(z)=\lim_{z\to 0}F(z+1)=F(1)$ so $z=0$ is a simple pole of $F(z)$ and continuing by (2) we see that $a_k=-k,\forall k\in\mathbb{N}$ are simple poles of $F(z)$.
Define $f(z):=\tfrac{1}{F(z+1)}$ so that $f(z)$ is entire, then by the Weierstrass' Factor Theorem
$$f(z)=f(0)e^{\tfrac{f(0)}{f^\prime (0)}z}\prod_{k=1}^\infty \left\{\left(1-\tfrac{z}{a_k}\right)e^{\tfrac{z}{a_k}}\right\}\quad \text{(eqn 1)}$$

and we have from the definition of $f(z)$ that $f(0)=\tfrac{1}{F(1)}$ and that $f^\prime (0) =-\tfrac{1}{\left[ F^\prime (1)\right] ^2}$ substituting all known values into (eqn 1) we get

$$\tfrac{1}{zF(z)}=\tfrac{1}{F(z+1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}$$

multiply by $z$ on both sides

$$\tfrac{1}{F(z)}=\tfrac{z}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}\quad (eqn 2)$$

set $z=1$ in the above

$$\tfrac{1}{F(1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}}\prod_{k=1}^\infty \left\{\left(1+\tfrac{1}{k}\right)e^{-\tfrac{1}{k}}\right\}$$

do some algebra to get

$$\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}=\lim_{N\to\infty}\sum_{k=1}^N\left[\log \left(1+\tfrac{1}{k}\right)-\tfrac{1}{k}\right]=-\gamma$$

by the definition of Euler's constant $\gamma$, substitute this into (eqn 2) and compare to the Weierstrass product definition of the Gamma function and we have arrived at the required result.

Ok, I see "some algebra" but could you at least elaborate the last lines? Especially as you nowhere mentioned which definition of the Gamma function you used. I have the impression that it takes me more effort to make your proof readable than it takes to give another one. Also Weierstrass needed a bit more explanation. I doubt that an average member can understand how you applied it to what.

 

[benorin]

Spoiler: problem #8

By (3) $\exists M :| F(x+iy) |< M,\forall x\in \left[ 1,2\right]$ and in particular $| F(1) | <M$, also by (2) $F(z)=\tfrac{1}{z} F(z+1)$ and hence F(z) is bounded in the half-plane $H(0)$. Also by (2) $\lim_{z\to 0} F(z)=\lim_{z\to 0}\tfrac{1}{z}F(z+1)=F(1)\lim_{z\to 0}\tfrac{1}{z}=\infty$ but $\lim_{z\to 0}zF(z)=\lim_{z\to 0}F(z+1)=F(1)$ so $z=0$ is a simple pole of $F(z)$ and continuing by (2) we see that $a_k=-k,\forall k\in\mathbb{N}$ are simple poles of $F(z)$.
Define $f(z):=\tfrac{1}{F(z+1)}$ so that $f(z)$ is entire, then by the Weierstrass' Factor Theorem
$$f(z)=f(0)e^{\tfrac{f(0)}{f^\prime (0)}z}\prod_{k=1}^\infty \left\{\left(1-\tfrac{z}{a_k}\right)e^{\tfrac{z}{a_k}}\right\}\quad \text{(eqn 1)}$$

and we have from the definition of $f(z)$ that $f(0)=\tfrac{1}{F(1)}$ and that $f^\prime (0) =-\tfrac{1}{\left[ F^\prime (1)\right] ^2}$ substituting all known values into (eqn 1) we get

$$\tfrac{1}{zF(z)}=\tfrac{1}{F(z+1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}$$

multiply by $z$ on both sides

$$\tfrac{1}{F(z)}=\tfrac{z}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right)e^{-\tfrac{z}{k}}\right\}\quad (eqn 2)$$

set $z=1$ in the above

$$\tfrac{1}{F(1)}=\tfrac{1}{F(1)}e^{-\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}}\prod_{k=1}^\infty \left\{\left(1+\tfrac{1}{k}\right)e^{-\tfrac{1}{k}}\right\}$$

do some algebra to get

$$\tfrac{F(1)}{\left[ F^\prime (1)\right] ^2}=\lim_{N\to\infty}\sum_{k=1}^N\left[\log \left(1+\tfrac{1}{k}\right)-\tfrac{1}{k}\right]=-\gamma$$
edit begins here:
by the definition of Euler's constant $\gamma$, substitute this into (eqn 2) and invert to get

$$\begin{gathered} \boxed{ F(z)=F(1)\cdot\tfrac{1}{z} e^{-\gamma z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right) ^{-1} e^{\tfrac{z}{k}}\right\} \\ =F(1)\cdot \Gamma (z) } \\ \end{gathered}$$

since the Weierstrass' product definition of the Gamma function is

$$\Gamma (z) =\tfrac{1}{z} e^{-\gamma z}\prod_{k=1}^\infty \left\{\left(1+\tfrac{z}{k}\right) ^{-1} e^{\tfrac{z}{k}}\right\} $$

we have arrived at the required result.

 

[TeethWhitener]

Spoiler: Problem 2

Maybe I'm misunderstanding the problem, but if we're only worried about continuity (and not differentiability), can't we just do something simple? I just built a parallelogram and let $f$ and $g$ take paths along opposite sides:

Let $f(\frac{3}{2})=\frac{3}{2}, g(\frac{3}{2})=\frac{3}{2}, f(\frac{1}{2})=\frac{1}{2}, g(\frac{1}{2})=\frac{1}{2}$. Notice that $\frac{1}{2}x+\frac{3}{4}$ and $2x-\frac{3}{2}$ both go through $(\frac{3}{2},\frac{3}{2})$, and $\frac{1}{2}x+\frac{1}{4}$ and $2x-\frac{1}{2}$ both go through $(\frac{1}{2},\frac{1}{2})$. We see that $2x-\frac{1}{2}$ intersects $\frac{1}{2}x+\frac{3}{4}$ at $(\frac{5}{6},\frac{7}{6})$, and $2x-\frac{3}{2}$ intersects $\frac{1}{2}x+\frac{1}{4}$ at $(\frac{7}{6},\frac{5}{6})$.

So now we just define:
$$f(x)=\begin{cases}
x &\text{if } 0\leq x < \frac{1}{2} \text{ or }\frac{1}{2} \leq x \leq 2\\
2x-\frac{1}{2} & \text{if } \frac{1}{2} \leq x < \frac{5}{6} \\
\frac{1}{2}x+\frac{3}{4}& \text{if } \frac{5}{6} \leq x < \frac{3}{2} \\
\end{cases}
$$
and
$$g(x)=\begin{cases}
x &\text{if } 0\leq x < \frac{1}{2} \text{ or }\frac{1}{2} \leq x \leq 2\\
\frac{1}{2}x+\frac{1}{4}& \text{if } \frac{1}{2} \leq x < \frac{7}{6} \\
2x-\frac{3}{2} & \text{if } \frac{7}{6} \leq x < \frac{3}{2} \\
\end{cases}
$$

 

[nuuskur]

Spoiler: Problem 1

Let K\subseteq \mathbb C be non-empty compact. Suppose \{\gamma_n \in K \mid n\in\mathbb N\} \subseteq K is dense in K\ \ (\mathbb C is separable). Let D : e_n\mapsto \gamma_ne_n be a diagonal operator (in the infinite case H\cong \mathbb C^\omega, otherwise H\cong \mathbb C^N).

For any n\in\mathbb N we have \gamma_n\in\sigma (D), because D-\gamma_n\mathrm{id} is not injective. If we look at the kernel, we have
<br /> \sum \lambda _k(D-z_n\mathrm{id})(e_k) = \sum _{k\neq n} (\lambda _k\gamma_k - \gamma _n)e_k + (\lambda_n -1)\gamma _n e_n = 0.<br />
We can clearly see \lambda _k \equiv 0 is not forced.

Since \sigma (D) is closed, we also have K\subseteq \sigma (D). On the other hand, suppose \lambda\notin K. Then
F \left ( \sum \lambda _ke_k\right ) := \sum\frac{\lambda _k}{\gamma _k-\lambda}e_k
is the inverse of D-\lambda \mathrm{id}, thus \lambda\notin \sigma (D). Indeed, we can check for basis elements. We have
<br /> (F \circ (D-\lambda \mathrm{id}))(e_k) = F((\gamma _k-\lambda)e_k) = \frac{\gamma _k-\lambda}{\gamma _k-\lambda}e_k = e_k<br />
and
<br /> ((D-\lambda \mathrm{id}) \circ F)(e_k) = (D-\lambda \mathrm{id}) \left ( \frac{1}{\gamma _k-\lambda}e_k \right ) = e_k.<br />
Altogether \sigma (D) = K.

 

[member 587159]

Spoiler: Problem 1

Let K\subseteq \mathbb C be non-empty compact. Suppose \{\gamma_n \in K \mid n\in\mathbb N\} \subseteq K is dense in K\ \ (\mathbb C is separable). Let D : e_n\mapsto \gamma_ne_n be a diagonal operator (in the infinite case H\cong \mathbb C^\omega, otherwise H\cong \mathbb C^N).

For any n\in\mathbb N we have \gamma_n\in\sigma (D), because D-\gamma_n\mathrm{id} is not injective. If we look at the kernel, we have
<br /> \sum \lambda _k(D-z_n\mathrm{id})(e_k) = \sum _{k\neq n} (\lambda _k\gamma_k - \gamma _n)e_k + (\lambda_n -1)\gamma _n e_n = 0.<br />
We can clearly see \lambda _k \equiv 0 is not forced.

Since \sigma (D) is closed, we also have K\subseteq \sigma (D). On the other hand, suppose \lambda\notin K. Then
F \left ( \sum \lambda _ke_k\right ) := \frac{\lambda _k}{\gamma _k-\lambda}e_k
is the inverse of D-\lambda \mathrm{id}, thus \lambda\notin \sigma (D). Indeed, we can check for basis elements. We have
<br /> (F \circ (D-\lambda \mathrm{id}))(e_k) = F((\gamma _k-\lambda)e_k) = \frac{\gamma _k-\lambda}{\gamma _k-\lambda}e_k = e_k<br />
and
<br /> ((D-\lambda \mathrm{id}) \circ F)(e_k) = (D-\lambda \mathrm{id}) \left ( \frac{1}{\gamma _k-\lambda}e_k \right ) = e_k.<br />
Altogether \sigma (D) = K.

Seems to work! Working with diagonal operators was also what I had in mind. Here is a more sophisticated approach using the theory of $C^*$-algebras:

Consider the $C^*$-algebra $C(K)$. Then the inclusion $i: K \to \Bbb{C}$ has spectrum $K$. Next, choose a Hilbert space $H$ and an injective $*$-homomorphism $\varphi: C(K) \to B(H)$ (GNS-construction). Then $\varphi(i)$ is a bounded operator on $H$ with spectrum $K$.

I will look at the other solution attempt soon.

 

[Infrared]

@TeethWhitener If I take $a=3/2$ and $b=1/2$ in your example, then $f(3/2)-f(1/2)=1$ and $g(3/2)-g(1/2)=1$ are both integers.

 

[nuuskur]

Spoiler: Problem 3

Suppose V/W is complete. Let x_n\in V,\ n\in\mathbb N, be a Cauchy sequence. Let \pi :V\to V/W be the projection, then \pi (x_n),\ n\in\mathbb N, is Cauchy in V/W. For some x\in V we have \pi (x_n) \xrightarrow[]{}\pi (x). By definition of infimum pick z_n\in V such that \|x_n-x-z_n\| \leq \|\pi (x_n-x)\| + \frac{1}{n},\ n\in\mathbb N. Then \|x_n-(x+z_n)\| \to 0. So we would have x_n \to x+\lim z_n. This is justified, because by triangle equality
<br /> \|z_n-z_m\| \leq \|x_n-x-z_n\| + \|x_n-x_m\| + \|x_m-x-z_m\| \xrightarrow[m,n\to\infty]{}0.<br />

 

[TeethWhitener]

@TeethWhitener If I take $a=3/2$ and $b=1/2$ in your example, then $f(3/2)-f(1/2)=1$ and $g(3/2)-g(1/2)=1$ are both integers.

I must have misread the question then. Are you looking for a proof that it's true for all $f,g$ given the problem constraints? I thought the question was just asking for an example.

 

[nuuskur]

I must have misread the question then. Are you looking for a proof that it's true for all $f,g$ given the problem constraints? I thought the question was just asking for an example.

Given arbitrary continuous maps f,g on [0,2] we are to show such a\neq b exist. I'm thinking Intermediate value theorem might help. Not sure, right now.

 

[nuuskur]

Spoiler: Problem 4

For every x\in\mathbb R we have \mathbb P\{X\leq x\}\in \{0,1\}. Let F be the distribution function for X. F is right continuous and we have \lim _{x\to\infty} F(x) = 1 and \lim _{x\to -\infty}F(x) = 0. This implies there exists c\in\mathbb R such that F = I_{[c,\infty]}. Now \mathbb P\{X&lt;c\} = F(c-) = 0, therefore X=c a.s.

Spoiler: Problem 4 #2 Kolmogorov 0-1

We have \mathbb P\{X\leq x\} \in\{0,1\} for every x\in\mathbb R. One readily verifies X is independent of itself. Put c:= \inf \{x\in\mathbb R \mid X\leq x\}. It is finite, because \lim _{x\to \infty} \mathbb P\{X\leq x\} = 1, therefore for sufficiently large x_0 we have \mathbb P\{X\leq x_0\}=1. By Kolmogorov's 0-1 law \mathbb P\{X=c\}=1.

Since X is almost surely constant, the probability it takes any other value is zero, hence its variance is zero. Therefore \mathbb E(X-\mathbb E(X))^2 = 0 implies X=\mathbb E(X) a.s. The first moment exists, because variance is finite.

.. by triangle equality

Triangle equality I meant triangle inequality.

 

[benorin]

Summary:: functional analysis, operator theory, topology, measure theory, calculus
Authors: Math_QED (MQ), Infrared (IR), Wrobel (WR), fresh_42 (FR).

9. Show that there exists no continuous function g:C∖{0}→C such that eg(z)=z for all z∈C∖{0} (i.e. there is no continuous logarithm on C∖{0}). (MQ)
(Corrected version, credits go to @PeroK for pointing out and solving the original problem.)

I beg to differ: A Course of Modern Analysis, 3rd ed. Whittaker & Watson pg 589 (heading A6) says $\log z = \Log |z| + i \arg z$ is a continuous multi-valued function of $z$ since $|z|$ is a continuous function of $z$.

 

[PeroK]

I beg to differ: A Course of Modern Analysis, 3rd ed. Whittaker & Watson pg 589 (heading A6) says $\log z = \Log |z| + i \arg z$ is a continuous multi-valued function of $z$ since $|z|$ is a continuous function of $z$.

I suspect you can make log continuous by taking the domain to be a set of complex planes disconnected at the branch cuts.

These are, of course, Riemann surfaces.

In any case it's $\arg z$ that is discontinuous.

 

[nuuskur]

Oh brother, this simply connected business for \mathbb C^* is simply not necessary. Let's go again.

Spoiler: Problem 9

Suppose g:\mathbb C^* \to \mathbb C is continuous with e^{g(z)} \equiv z. Then g is holomorphic, because the exponential map is holomorphic and
<br /> \lim _{z\to z_0} \frac{g(z) - g(z_0)}{z-z_0} = \lim _{g(z)\to g(z_0)} \frac{g(z)-g(z_0)}{e^{g(z)} - e^{g(z_0)}}.<br />
By differentiating we get 1 = g&#039;(z) e^{g(z)} = zg&#039;(z), which implies g&#039;(z) = \frac{1}{z} on \mathbb C^*. But now by Cauchy's integral theorem, we get
<br /> 0 = \oint _{|z|=1} g&#039;(z) dz = \oint_{|z|=1} \frac{1}{z} dz = 2i\pi.<br />
Thus, such a g cannot exist.

Maybe I'm hunting a fly with a 50 cal rifle with armor-piercing rounds..

We can kill a fly with a fly swatter. Don't need the rifle.

Spoiler: Problem 9

Suppose g:\mathbb C^* \to\mathbb C is continuous and satisfies the identity e^{g(z)} = z. Since g is right inverse to \exp, it is injective, thus g(\mathbb C^*) \cong \mathbb C^*. But now \exp is forced to be injective on \mathbb C^*. Indeed, for any u,v\neq 0 we have
e^u = e^v \Leftrightarrow e^{g(z)} = e^{g(w)} \Leftrightarrow z=w \Rightarrow u=v.
But that's impossible.

 

[Infrared]

@nuuskur Where did you use continuity (this is definitely a necessary condition)? Anyway, you seem to be claiming that $g$ is surjective in saying $g(\mathbb{C}^*)=\mathbb{C}^*$. How do you know this? If you only mean that $g$ gives a bijection from $\mathbb{C}^*$ to its image, then how are you writing $u=g(z), v=g(w)$?

 

[member 587159]

If we try to make $\beta$ continuous, then without loss of generality we can take $\beta(0) = 0$, hence $\beta = \theta$ and we get a discontinuity at $\theta = 0$. More generally, for any $\phi$ we could could take $\beta(\phi) = \phi + 2n\pi$ and get the discontinuous branch cut at $\theta = \phi$.

Hmm, I need a little more details here. Explain why the discontinuities arise. I find your argument a bit too handwavy.

 

[nuuskur]

@nuuskur Where did you use continuity (this is definitely a necessary condition)? Anyway, you seem to be claiming that $g$ is surjective in saying $g(\mathbb{C}^*)=\mathbb{C}^*$. How do you know this?

Continuity is implicit. I'm working in the category with continuous maps. No, g is injective, therefore it's an isomorphism onto its image.

 

[Infrared]

Continuity is implicit.

Which part of your argument fails if $g$ is not required to be continuous?

No, g is injective, therefore it's an isomorphism onto its image.

Please explain this line.

e^u = e^v \Leftrightarrow e^{g(z)} = e^{g(w)} \Leftrightarrow z=w \Rightarrow u=v.

What are $z$ and $w$ in relation to $u$ and $v$? It looks to me like you're assuming that $g$ is surjective here (by saying that you can write $u=g(z), v=g(w)$)

 

[member 587159]

Continuity is implicit. I'm working in the category with continuous maps. No, g is injective, therefore it's an isomorphism onto its image.

You really need that $g(\Bbb{C}^*) = \Bbb{C}^*$ for your argument to work. Also, when using the symbol $\cong$, explain what you mean with the symbol. I assume that you mean isomorphism in the category of continuous maps, but how are you even sure the inverse on the image is continuous as well?