Max Force for Sliding Blocks: Solving a Tricky Force Problem - FBD Included

[NasuSama]

Homework Statement

Small block 1 with mass m = 2.56 kg sits on top of large block 2 of mass M = 7.7 kg, and the pair sit on a frictionless, horizontal table. Between the blocks: the coefficient of kinetic friction is μk = 0.146, and the coefficient of static friction is μ_s = 0.203.

Find the magnitude of the maximum force applied horizontally to the upper block (block 1) that will cause the two blocks to slide together.

Homework Equations

Some ideas I have are:

→Σ F_up = Σ F_down
→Σ F_left = Σ F_right
→F = ma [Obviously]
→F_r = µ_k * F_N

The Attempt at a Solution

Just the free body diagram. See attached file. I am not sure about the down vertical component. I know that mg must point down, but what about the big M? Does that play the significant role for such problem?

I can't seem to find the next correct steps here.

 

[NasuSama]

Something more I can add.

F_N = mg
F_r = µ_k * F_N = µ_k * mg = ma

But I can't figure out the equations for the system of larger M mass with the m mass on the top.

 

[PhanthomJay]

If the 2 blocks slide together, they must both accelerate at the same rate, and and will do so only if the top block does not slide with respect to the bottom block.
You should draw a FBD of each block, identify all the forces acting on each (remembering Newton's 3rd law), and apply Newton's 2nd law to each block. You will then have to solve the resulting 2 equations with the 2 unknowns and F to solve for them. Is kinetic or static friction at play here?

 

[azizlwl]

Small block 1 with mass m = 2.56 kg sits on top of large block 2 of mass M = 7.7 kg, and the pair sit on a frictionless, horizontal table. Between the blocks: the coefficient of kinetic friction is μk = 0.146, and the coefficient of static friction is μ_s = 0.203.

Find the magnitude of the maximum force applied horizontally to the upper block (block 1) that will cause the two blocks to slide together.
-----------------------------------------
The maximum force that can be applied to lower block is Nμ_s.
This is the maximum acceleration of the lower block.
The maximum force will produce maximum acceleration of both blocks.

You can subtitute this as 2 blocks with a string attach between them with Nμ_s breaking point. A force will accelerate both until the breaking point.

 

[NasuSama]

If the 2 blocks slide together, they must both accelerate at the same rate, and and will do so only if the top block does not slide with respect to the bottom block.
You should draw a FBD of each block, identify all the forces acting on each (remembering Newton's 3rd law), and apply Newton's 2nd law to each block. You will then have to solve the resulting 2 equations with the 2 unknowns and F to solve for them. Is kinetic or static friction at play here?

I believe kinetic friction plays for this problem.

I know much about the horizontal components of the small box, but not sure where to start.

 

[PhanthomJay]

I believe kinetic friction plays for this problem.

I know much about the horizontal components of the small box, but not sure where to start.

There is no friction between the table and lower box, so friction does not exist at this interface. However, there is friction between the top and lower box, and it is asked to determine the max force that can be applied to the top block without the top block slipping with respect to the lower box. Slipping cannot occur until the max static friction force between the two boxes is exceeded.

So draw a free body diagram of the top block only. Identify all four forces acting on it (theer are 2 in the horizontal direction..what are they? and there are 2 in the vertical direction..what are they?), determine the max available friction force, and apply Newton 2 in the x direction. You will get an equation with 2 unknowns, F and a.

Then you should draw a FBD of the lower block, identify all forces acting on it, and apply Newton 2 to this block, in the x direction. That will allow you to solve for the acceleration of the lower block, which is the same as the acceleration of the upper one, since it is given that they move together. Once you know a, solve for F in the first equation.

As a check, you should draw a FBD of the system of both blocks together, which you can do since they accelerate as one unit. Friction does not enter into this FBD since it is internal to the system. Then use Newton 2 on the system of blocks, using both masses combined, to check your results for a nd F.

 

[NasuSama]

There is no friction between the table and lower box, so friction does not exist at this interface. However, there is friction between the top and lower box, and it is asked to determine the max force that can be applied to the top block without the top block slipping with respect to the lower box. Slipping cannot occur until the max static friction force between the two boxes is exceeded.

So draw a free body diagram of the top block only. Identify all four forces acting on it (theer are 2 in the horizontal direction..what are they? and there are 2 in the vertical direction..what are they?), determine the max available friction force, and apply Newton 2 in the x direction. You will get an equation with 2 unknowns, F and a.

Then you should draw a FBD of the lower block, identify all forces acting on it, and apply Newton 2 to this block, in the x direction. That will allow you to solve for the acceleration of the lower block, which is the same as the acceleration of the upper one, since it is given that they move together. Once you know a, solve for F in the first equation.

As a check, you should draw a FBD of the system of both blocks together, which you can do since they accelerate as one unit. Friction does not enter into this FBD since it is internal to the system. Then use Newton 2 on the system of blocks, using both masses combined, to check your results for a nd F.

Here is the diagram I drew...

 

[PhanthomJay]

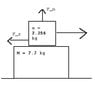
Here is the diagram I drew...

You should show the forces and their directions at the locations where they act.

TOP BOX:

1. In your FBD of the top box, the gravity force, which is the weight of the block, mg, acts down. You have correctly identified this force and its direction, but you should show it acting down originating from the center of the block, not at the bottom.
2. You have also correctly identified the normal force, F_n, and its direction, but you should show it acting up on the bottom of the block, since that is the surface it acts on. Since there is no acceleration in the y direction, Newton 1 tells you that the F_n = mg.
3. You have also correctly identified the friction force, F_r, and its direction, but you should show it acting along the bottom of the box, since that is the surface it acts on. Also, the friction force is u_s(F_n), not u_s(mg), but the result is the same since F_n = mg.
4. You have correctly identified the applied force, call it F_app, and shown its location correctly, but the applied force, F_app, is not equal to ma. The net force in the x direction is equal to ma, where the net force is the applied force minus the friction force.

So now write Newton's 2nd law in the x direction, and put some numbers on it for the known values. This is equation 1.

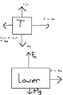
BOTTOM BOX:

1. The weight of the lower box is Mg, acting down , OK.
2. There is the normal force from the upper box, F_n, acting on the top of the lower box, but it acts down, per Newton 3.
3. There is also a normal force, N, of the table on the box, acting up on the bottom of the box. You didn't show that force.
4. You show a force F acting on the right of the box. No such force exists.
5. You have neglected to show the friction force acting on the top of the block. From Newton 3, it is equal and opposite to the friction force acting on the top block. This is key.

So now write Newton 2 in the x direction. Only the friction force acts in the x direction. Solve for a, and plug it into the first equation to solve for the applied force F_app.

 

[azizlwl]

Find the magnitude of the maximum force applied horizontally to the upper block (block 1) that will cause the two blocks to slide together.
----------------
1. the two blocks to slide together implied F=(M+m)a ...(1)
2. The maximum force that can pull the lower block is mgμ_s
Ma=mgμ_s ...(2)

Add:
If there is slippage, maximum acceleration of M, a_sliding;
Ma_sliding=mgμ_k

The frictional force experienced by lower block is equal and opposite to that experience by the upper block.
This forward frictional force(relatively it is moving backward from upper block) that pulls it forward until maximum frictional force.

 

[NasuSama]

I found Jay's advice to be pretty good, which helps me learn how to apply some concept, but azizl gave away the answer.

Thank you everyone who helped me for this problem!