Minimum seperation of two electrons moving toward each other

In summary, the minimum separation of two electrons moving toward each other is determined by the Coulomb force, which is inversely proportional to the square of the distance between the two electrons. This separation is important because it affects the stability and behavior of atoms and molecules, and can be calculated using Coulomb's law. The minimum separation can change depending on external forces and is directly related to the energy of the electrons.
  • #1
physicks885
1
1
Homework Statement
Two electrons approach each other moving in opposite directions. When the separation between the electrons is 10 m, the two electrons move with the same speed of 𝑣=38 m/s. What is the minimum distance that the electrons will approach each other before they begin to move away due to the effect of electrical repulsion?
Relevant Equations
K.E = U
[Mentor Note -- Two threads started by partners in a class have been merged into this one thread, since they are working on a shared solution to turn in]

1647733226499.png
 
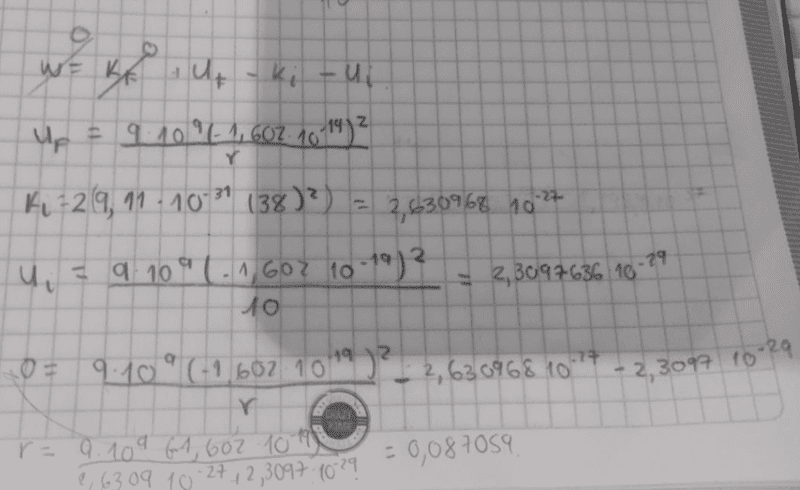
Last edited by a moderator:
  • Like
Likes kareenlama
Physics news on Phys.org
  • #2
WhatsApp Image 2022-03-19 at 6.37.10 PM.jpeg
 
  • #3
It looks like you have the correct idea. I strongly recommend that you redo the problem using symbols exclusively in order to find an algebraic expression for the minimum separation ##r##. Once you have that, you can substitute numbers at the very end. This eliminates copying and round-off errors and preserves your sanity.
 
  • Informative
  • Like
Likes physicks885 and kareenlama
  • #4
Locked pending moderation
 
  • Haha
Likes physicks885
  • #5
Thread is now re-opened after sorting out the confusing two-user issue. :smile:
 
  • Like
Likes SammyS

1. What is the minimum separation between two electrons moving toward each other?

The minimum separation between two electrons moving toward each other is dependent on their initial velocities and the strength of their electric charges. It can be calculated using Coulomb's Law, which states that the force between two charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.

2. How does the minimum separation between two electrons affect their interactions?

The minimum separation between two electrons determines the strength of their interactions. If the separation is too small, the repulsive force between the electrons will be greater than the attractive force, causing them to repel each other. This can lead to a scattering or deflection of their paths.

3. Can the minimum separation between two electrons ever be zero?

No, the minimum separation between two electrons cannot be zero. As they approach each other, the repulsive force between them will increase, preventing them from getting any closer. This is due to the Pauli exclusion principle, which states that no two electrons can occupy the same quantum state simultaneously.

4. How does temperature affect the minimum separation between two electrons?

Temperature does not directly affect the minimum separation between two electrons. However, at higher temperatures, the electrons will have more kinetic energy and will be moving faster, which can result in a larger minimum separation between them.

5. Is the minimum separation between two electrons a constant value?

No, the minimum separation between two electrons is not a constant value. It can vary depending on the initial conditions of the electrons, such as their velocities and charges. It can also change over time as the electrons interact with other particles in their surroundings.

Similar threads

Electrons and their little role in nuclear physics
    • Introductory Physics Homework Help
Replies
1
Views
752
Dual electron repulsion (momentum question)
    • Introductory Physics Homework Help
Replies
7
Views
4K
Kinetic Energy of Colliding Protons
    • Introductory Physics Homework Help
2
Replies
54
Views
8K
I About the repulsive force between two electrons
    • Quantum Physics
Replies
7
Views
1K
Two networks described by v-i graph: Find voltages when interconnected
    • Introductory Physics Homework Help
Replies
1
Views
439
Given current and density of electrons, what is their speed?
    • Introductory Physics Homework Help
Replies
2
Views
1K
Two electrons are fired at each other
    • Introductory Physics Homework Help
Replies
11
Views
13K
Two electrons repel each other and gain velocity
    • Introductory Physics Homework Help
Replies
10
Views
3K
Two cars driving toward each other (non-uniform speed)
    • Introductory Physics Homework Help
Replies
5
Views
7K
What's the chemistry behind a semiconductor?
    • Chemistry
Replies
8
Views
991

Hot Threads

Recent Insights

Back
Top