B Understanding Minkowski Diagrams in Special Relativity

[jannesvanpoppelen]

Something that has been bothering me for a while is this question. As seen from this Minkowski diagram,http://imgur.com/GkBN2HQ , the angle between x and x' is equally big as the angle between ct and ct'. I really can't seem to figure out why this is, although I think it has to do with the second postulate of special relativity, which is "The speed of light in free space has the same value c in all inertial frames of reference". Is there anyone here that might be able to help me? Kind regards (English is not my native language. Sorry)

 

[Orodruin]

The postulates of SR lead to the Lorentz transformations:
$$ ct' = \gamma(ct - vx/c) $$
$$ x' = \gamma(x - vct/c)$$
The $t'$ axis is given by $t' = 0$ and so for this axis $ct = (v/c)x$. The $x'$ axis is instead given by $x' = 0$ leading to $ct = (c/v)x$. Therefore the slope of the $x'$ axis is the reciprocal of the slope of the $t'$ axis, which means they must be the same angle from the $x$ and $t$ axes, respectively.

 

[m4r35n357]

Something that has been bothering me for a while is this question. As seen from this Minkowski diagram,http://imgur.com/GkBN2HQ , the angle between x and x' is equally big as the angle between ct and ct'. I really can't seem to figure out why this is, although I think it has to do with the second postulate of special relativity, which is "The speed of light in free space has the same value c in all inertial frames of reference". Is there anyone here that might be able to help me? Kind regards (English is not my native language. Sorry)

There seems to be a good answer (not mine!) on Reddit ;)

 

[jannesvanpoppelen]

There seems to be a good answer (not mine!) on Reddit ;)

Yeah, I asked it on reddit aswell, yet I am basically a newcommer on SR and I don't really have a clue what is meant by that. Maybe that you can elaborate any further?

 

[robphy]

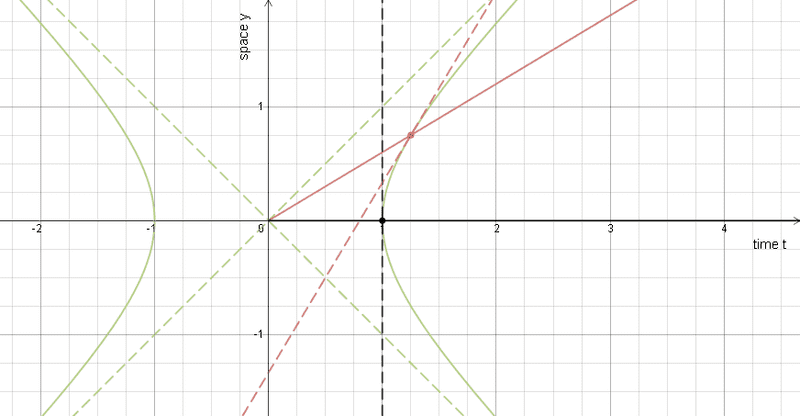
Here's a diagram to go along with @Orodruin 's reply.
https://www.desmos.com/calculator/ti58l2sair [my t axis is horizontal ]

The Lorentz Transformations mentioned above preserves the unit hyperbola (that is, under that Lorentz Transformation, the events on the future unit hyperbola are mapped to the same hyperbola), whose asymptotes are lightlike---that is to say, all frames of reference agree on the same value of the speed of light (maximum signal speed).

An inertial worldline (the t'-axis) drawn from the "center" of the hyperbola into the future light cone intersects the hyperbola at an event.
Think of this worldline as a radius vector from the center.
The tangent line to the hyperbola here is "spacetime-perpendicular" (perpendicular in Minkowski spacetime geometry) to the worldline.
Think "tangent to a circle is perpendicular to radius".
Physically, this tangent line determines the x'-axis... That observer's "space" direction is perpendicular to that observer's "time" direction.
Additionally, this tangent line has the "same value of t' " for that observer---this is that observer's line of simultaneity.

Try changing the E-slider... to the Euclidean case (when E= -1) and the Galilean case (when E=0).Now there is another way to think about this using a "clock diamond" (shameless plug for my Insights article) and its diagonals.
Here is a geogebra diagram from
https://www.physicsforums.com/threads/spacetime-diagrams-of-light-clocks-comments.875884/
https://www.geogebra.org/m/Jq4jDMRW
https://www.geogebra.org/files/00/03/71/96/material-3719659-thumb.png?v=1466261681

 

[jannesvanpoppelen]

its updated from I to B now, sorry I am new here

 

[Ibix]

It's related to why the angle between x and x' is the same as the angle between y and y' when the primed and unprimed coordinates are related by a rotation. The Lorentz transforms are rotations that do not follow the rules of Euclidean geometry, but rather hyperbolic geometry.

I'm not sure there's really any more to it than that. A Minkowski diagram isn't really what spacetime looks like (assuming "what it looks like" is even a coherent concept). It is, however, a good visualisation and symmetries in the reality are reflected in the visualisation

 

[robphy]

Your diagram shows a portion of a causal diamond.
But here's how to think about the x'-axis.
First use units so that light signals are at 45 degrees.

When an observer sends out a light signal and receives its echo,
the event that reflected the signal is, according that observer, simultaneous with the halfway time between sending and receiving. That is, if the observer sent out a light signal at t'=4 sec and received its echo at t'=6 sec, the reflecting event Q must have occurred at t'=5 sec... (at x'=1 light sec). So where is this Q? Draw a forward in space light signal at 45 degrees from the emission event. Where to stop? From the reception event, draw a light signal that arrives from the past from forward in space. The intersection gives Q. The diagram you posted did exactly this by sending at A, reflecting at B, and receiving at C.

The x'-axis is parallel to the line that joins B to the midpoint-event D on the observer worldline between emission at A and reception at C. That line is dotted on your diagram.

The t' and x' axes are reflections about the forward light signal. So the angles are equal.

 

[arydberg]

This should explain what you want.

Al

http://richardhaskell.com/files/Special Relativity and Maxwells Equations.pdf

 

[robphy]

This should explain what you want.

Al

http://richardhaskell.com/files/Special Relativity and Maxwells Equations.pdf

That uses Brehme diagrams. I don't think that this document will be helpful.