- #1
fee_de
- 3
- 4
- TL;DR Summary
- I don't understand a spacetime diagram about relativty and simultaneity that I found in a book and its explaination by the author
I'm reading a book called "Reality is not what it seems: the journey to quantum gravity" by Carlo Rovelli and I'm struggling to understand this diagram that is part of the chapter about special relativity.
https://i.stack.imgur.com/JgBDJ.jpg
Before this image Rovelli writes:
"It's not possible to have a satisfying conversation from Earth to Mars. If I'm on Mars and you are here, I ask you a question, you answer as soon as you hear what I told you and I receive your answer 15 minutes after I asked you the question. This quarter of an hour of mine is time that is neither past nor future as compared to the moment when you answered. This implies that you can't say that an event on Mars is happening "now" because "now" does not exist".
I understand this concept, but then the author adds a footnote:
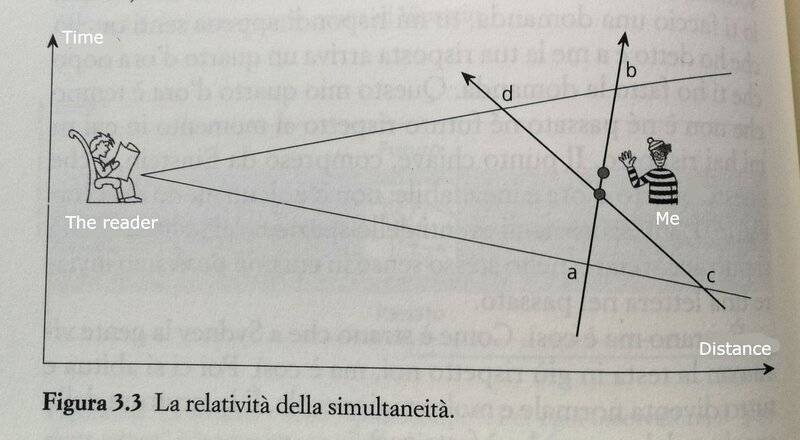
"The astute reader will object that the moment in the middle of my quarter of an hour can be considered simultaneus to your answer. The reader who studied physics may recognize that this is the "Einstein convention" to define simultaneity. However, this definition depends on the way I move, so it doesn't define simultaneity directly between two events, but only a simultaneity that is relative to the motion of specific bodies. In picture 3.3 (the diagram I attached), a dot is halfway between a and b, the points where I exit the past of the observer and I enter his future. the other dot is halfway between c and d, the points where I exit the past of the observer and I enter his future if I follow a different path. Both the dots are simultaneous to the reader, following this definition of simultaneity; however, they happen one after the other. The two dots are both simultaneous to the reader, but relatively to two different motions."
(I'm reading this book in Italian so I had to translate the paragraph, I'm sorry if it's not faultless).
First of all I don't understand what it means that "the moment in the middle of my quarter of an hour can be considered simultaneus to your answer". I tried to draw diagrams, I'm really struggling but I can't grab the concept. Talking about the diagram, why can we say that the observer perceives the two dots as simultaneous? They don't exit his past and enter his future at the same time, do they? In these diagrams souldn't we find simultaneous events on the same horizontal line?
I'm completely stuck, I would be very grateful if you could help me.
[Mentor Note -- Image attached to post from the OP's link]
https://i.stack.imgur.com/JgBDJ.jpg
Before this image Rovelli writes:
"It's not possible to have a satisfying conversation from Earth to Mars. If I'm on Mars and you are here, I ask you a question, you answer as soon as you hear what I told you and I receive your answer 15 minutes after I asked you the question. This quarter of an hour of mine is time that is neither past nor future as compared to the moment when you answered. This implies that you can't say that an event on Mars is happening "now" because "now" does not exist".
I understand this concept, but then the author adds a footnote:
"The astute reader will object that the moment in the middle of my quarter of an hour can be considered simultaneus to your answer. The reader who studied physics may recognize that this is the "Einstein convention" to define simultaneity. However, this definition depends on the way I move, so it doesn't define simultaneity directly between two events, but only a simultaneity that is relative to the motion of specific bodies. In picture 3.3 (the diagram I attached), a dot is halfway between a and b, the points where I exit the past of the observer and I enter his future. the other dot is halfway between c and d, the points where I exit the past of the observer and I enter his future if I follow a different path. Both the dots are simultaneous to the reader, following this definition of simultaneity; however, they happen one after the other. The two dots are both simultaneous to the reader, but relatively to two different motions."
(I'm reading this book in Italian so I had to translate the paragraph, I'm sorry if it's not faultless).
First of all I don't understand what it means that "the moment in the middle of my quarter of an hour can be considered simultaneus to your answer". I tried to draw diagrams, I'm really struggling but I can't grab the concept. Talking about the diagram, why can we say that the observer perceives the two dots as simultaneous? They don't exit his past and enter his future at the same time, do they? In these diagrams souldn't we find simultaneous events on the same horizontal line?
I'm completely stuck, I would be very grateful if you could help me.
[Mentor Note -- Image attached to post from the OP's link]
Last edited by a moderator: