MechE
- 5
- 0
Hi there!
There is a technique that is being used by my lecturer for mechanisms course at uni and i could not understand how this technique is manipulated.I wish i would know this methods name but no chance!.
This technique is being used to find normal acceleration of link in 4-bar mechanism.Manipulation:If you know the velocity of a link then draw a semi circle whose diameter is link's length and draw another circle whose radius is velocity vector and intersect these two circles then you obtain the normal acceleration of link.
What is the name of this method?
How can i find more examples on this method?
Thank you very much!
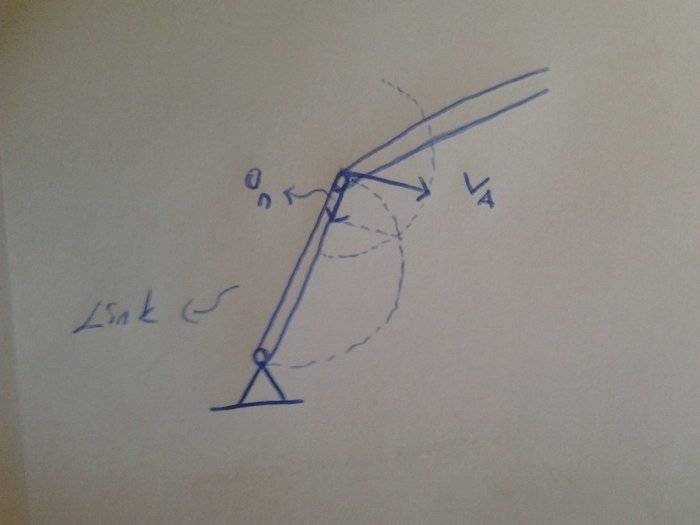
There is a technique that is being used by my lecturer for mechanisms course at uni and i could not understand how this technique is manipulated.I wish i would know this methods name but no chance!.
This technique is being used to find normal acceleration of link in 4-bar mechanism.Manipulation:If you know the velocity of a link then draw a semi circle whose diameter is link's length and draw another circle whose radius is velocity vector and intersect these two circles then you obtain the normal acceleration of link.
What is the name of this method?
How can i find more examples on this method?
Thank you very much!
Last edited: