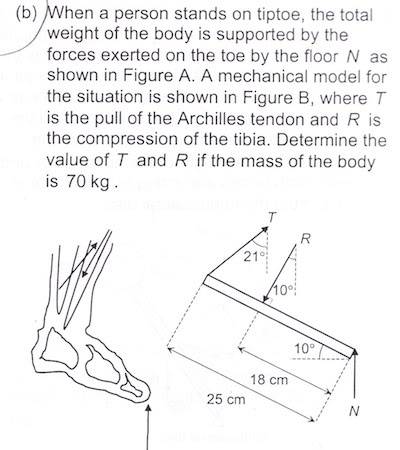
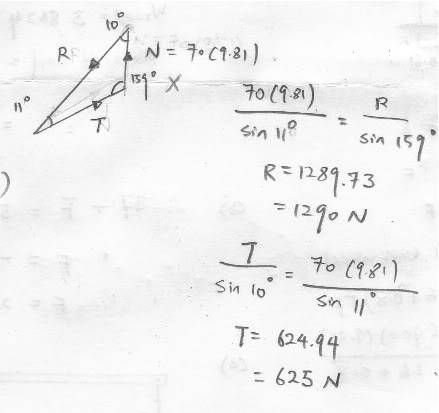
arkofnoah said:
But you're working backwards! I can also assumed that the horizontal component of R and T cancel out each other and therefore there is no need for friction to balance the forces? Why can't I assume that? In fact that's what I did when I use the vector-sum method (which is wrong I know but is friction really the reason?) Is it NECESSARY for such a system to have friction (since the question didn't specify)? I can totally imagine a ice ballerina tiptoeing on ice without accelerating forward.But what if I take R as the pivot point, which is what I did in one of the steps to calculate the values above. The friction needs to be factored into the calculation and I didn't and still arrive at the supposedly right answer!
It is not necessary, if you don't mind rotating without accelerating linearly.
Calculate the net torque for your special case with no friction, you will see that it is non-zero, and therefore you have not found the values for equilibrium.
Your answer is only supposedly right. It is in fact, incorrect, as it does not give 0 torque about any axis, as it must for equilibrium to hold.
Just because you can find specific values for the force under certain assumptions for translational equilibrium, does not mean that rotational equilibrium entails. Just like with the table example, there has to be some load distribution for it not to tip over, and if you move the legs too much, it won't be able to hold up.
In your table example, you can add the vectors up, but you cannot assume symmetry. Let's analyze that situation for a second. Let's assume, for simplicity, a square table with a side of length 2b.
Let's say we displace one of the legs to the center, the others remaining in their places.
Diagram:
1-------
|||||||||
||||4||||
|||||||||
2-------3
With the numbers standing in for the position of each of the legs.
You'll be 100% correct in saying Mg=N_1+N_2+N_3+N_4, having taken the vector sum, but that won't give you too much information.
You have to take the torques about some axis to see what the condition for equilibrium is, and you'll have to take frictions into account as well, since without them the system may be unstable.
Tusike said:
I think the answer lies in the fact that that really isn't a good model for standing on your toes. Just try it! There are actually two points where you're feet touches the ground, the tip of you're toes and where they leave your foot.
The model IS an accurate representation for when you are standing on your heels. And yes, just stand on your heels, and notice that unless you stand in a specific way (meaning your center of mass is just above your heels), you will fall! And the angles given in this problem aren't one of those ways..
Yes, when you look at the body as whole, there's a whole different condition required, for the external reaction force and the weight to be on the same line of force, but granting that separate equilibrium condition, we are now focusing solely on the foot.
Tusike said:
NOTE: You can only take the place where N is (the toe touches the ground) as the pivot point! For example, if you had a car wheel, the center of it is the only place where you could take the pivot point, you can't just take it wherever you want...:)
The above is not true if the body isn't attached to anything. For example, if you look at a ruler on a table that has been hit, you can take the pivot point for it's rotation wherever you want to calculate it's spin speed.
Hurr, isn't that the other way around? You can take any axis for a static situation, since \Sigma \vec \tau=0 about any axis in equilibrium, but for a dynamic situation, unless you want to deal with accelerated reference frames, and adjusting your moment of inertia to account for not taking the torques about the pivot or the center of mass, you end up in a mess, don't you? I mean, I think it's valid to find the angular velocity using any axis, but just way too much work compared to the comfy axes of the system.
I crunched the numbers with a frictional force at the point of contact, and for mechanical equilibrium it must be non-zero, and pointing to the right. I only had to take torques about the point of contact.
Looking back at the sheet I worked on, I see that the horizontal component equation for Newton's Second Law is redundant, unless we actually want to know the value of the frictional force. It is sufficient to look at the vertical components and the torque about the pivot point.
Looking at the torque about T or R would only complicate things by forcing us to consider the nature and value of the frictional force.
Tusike said:
Let's stop arguing about this... If an object is at rest, that can only be possible if the forces acting on it are 0, and if the torque's acting on it are 0. Both need to apply. (and even this way, sometimes an object isn't at rest, for example a spinning wheel may spin at a constant speed if all those are true) [/tex]
I disagree. :) Arguing is the quintessence of science and learning. Unless we pit all the ideas against each-other and pick out only those that survive, we wouldn't be making much progress, just stagnating.
Anyway, the situation you referred to is called dynamical equilibrium. Where the components in a system are moving with constant velocities but not accelerating. Remember Newton's First Law, an object in motion tends to stay in motion unless acted upon by an outside force.
That statement defines force in the way Newton's Second Law defines it, \vec F= m\vec a, it is what changes the velocity of an object with mass.
If you wish to look at it mathematically, F=ma = m\frac{dv}{dt}
\Delta v=\int_{t_0}^{t'}a \cdot dt = \int_{v_0}^{v'} dv=v'-v_0
Obviously, if the acceleration is 0, then the first integral is 0, implying v'=v_0, that is, the velocity goes unchanged.