Kotten
- 3
- 0
Homework Statement
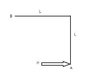
The L-shaped bar of mass m is lying on the horizontal surface when the force P is applied at A as shown. Determine the initial acceleration of point A. Neglect friction and the thickness of the bar.
(Sorry, don´t know how to get you a better picture)
L
B----------------
I
I L
I
P--------> I
A
Homework Equations
G=1/M*Sum(m_i*r_i) (a)
Sum(F_x)=ma_(Gx) (b)
Sum(F_y)=ma_(Gy) (c)
Sum(M_G)=I_G*alpha (d)
The Attempt at a Solution
I have calculated the center of mass, using eq (a), and got (from the bend of the bar)
G= -L/4 i -L/4 j
I also used eq (b) to get
P=ma_(Gx) ---> a_(Gx)=P/m
(c) gave
0=ma_(Gy) ---> a_(Gy)=0
and from (d) i got
P*3/4*L=I_G*alpha ---> alpha=(3PL)/(4*I_G )
And then I guess I have to calculate the moment of inertia for the figure, but I don´t know how to do that :/ Also I´m a bit confused, because this seems to me like a way to solve this problem, the chapter on how to calculate momento of inertia comes after this in the book. Is there another way to solve it? Or is this wrong and I´m missing something?