symbolic
- 2
- 0
Homework Statement
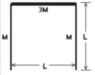
Three slim rods with the same length L are placed in a inverted U shape, as the figure shows. The masses of the vertical rods are the same, while the third bar has the mass 3 times bigger than the first or the second rod. The rods' thickness should be ignored. Find the moment of inercia of the system in relation to the following axes:
(a) containing each bar;
(b) parallel to the plane of the page and perpendicular to the bars, going through their centers of mass;
(c) perpendicular to the plane of the page, going through the center of mass of each bar;
(d) perpendicular to the plane of the page, going through the center of mass of the system xCM = L / 2 and yCM = 4 L / 5 taking the origin as the lowest point in the left vertical bar;
Answers: (a) 2 ML2, (2/3) ML2 e 2 ML2 ; (b) (11/12) ML2 e (3/4) ML2; (c) (35/12) ML2 , (17/12) ML2 e (35/12) ML2; (d) (73/60) ML2.
(question was translated, let me know if something is difficult to understand)
Homework Equations


The Attempt at a Solution
I tried to solve question (a) considering each bar as a point, that failed however.
Calculating Icm of the first bar with an axis going through it
Icm = M(0²) + 3M(L/2)² + M(M(0²)
Icm = 3/4ML²
I tried a few variations of this but couldn't reach the answer 2 ML2, so now I'm stuck.
 Any help is appreciated.
Any help is appreciated.