Aditya1998
- 1
- 0
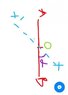
1. The problem statementα, all variables and given/known data
The moment of inertia of a Rod over an
Axis XX' passing through the center of mass of the Rod at an angle α is-
Moment of Inertia of Rod about the end, I =ML2/3
I=ML2/3
Answer of the question is ML2/3sin2α
I didn't understood how sin2 came because even if we shift OL over the axis XX' then
OX=OLcosα
[/B]
The moment of inertia of a Rod over an
Axis XX' passing through the center of mass of the Rod at an angle α is-
Homework Equations
Moment of Inertia of Rod about the end, I =ML2/3
The Attempt at a Solution
I=ML2/3
Answer of the question is ML2/3sin2α
I didn't understood how sin2 came because even if we shift OL over the axis XX' then
OX=OLcosα
[/B]