Moments and Couples: Find the Moment of 200N Force

[SUCRALOSE]

Could someone take a look at what I am working on and tell me if I am on the right track?

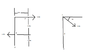
#1: Determine the moment of the 200 N force about point B. Please see attached picture for FBD.

First I find the x and y components.

x = 100N y= 173.2N, which are perpendicular and parallel to AB.

Then I find the distance of the 15° angle.

sin15(.5) = 0.13m
cos15(.5) = 0.48

So, now I add the forces to determine the moment about point B.

Mβ = +(173.2)(.48) - (100)(.13) = 70.1 N.M c.c.w

It would be of great appreciation is someone could help me.
Thank you.

 

[SUCRALOSE]

2: Says, replace the two 5 KN forces with an equivalent system consisting of the 7 KN force applied at C and a second force applied at point D. Determine the magnitude and direction of the second force and the distance CD.

Please see the picture for the FBD.

How I did this.

First I found the moment about point O for the two 5 KN forces.

Mo = -(5KN)(3m) + (5KN)(1.5m) = -7.5 KN.M c.w

Then I found the x and y components for the 7 KN force.

7(cos30) = 6.06 KN 7(sin30) = 3.5KN

Next I placed the 6.06 KN and 3.5KN force at point D and solve the moment about point C,( Cancelling those forces) and rearranging for the distance CD.

Mc = (3.5)(0) - (6.06)(d) = -7.5 KN.M

d = -7.5 - (3.5)(0) / -6.06 = 1.24 m

So, Magnitude = 6.06KN c.w. and CD = 1.24m