Energize
- 30
- 0
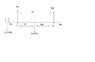
Ok I have this question where there is a beam 12m long, there is a pivot 3m along the beam (A) and another 10m along the beam (B). There is an elephant at the left end of the beam that weighs 10,000N and the weight of the beam is 4000N, I need to plot a graph of the distance moved (m) against the resultant of A. Now I know how to get the resultant of A when the object is in between the 2 pivots, but how do I work out the resultant of A when the object is not in between the 2 pivots?
Attachments
Last edited: