Monkey force diagram and tension problem

In summary, a monkey force diagram is a visual representation of the forces acting on a monkey or an object being held by a monkey. To draw one, you must identify all external forces, draw a dot and arrows, and label each force with a scale. Tension is a force transmitted through a string, represented by arrows pointing away from the object, and can be calculated using various methods. Drawing a monkey force diagram is important for visualizing and understanding forces, accurately calculating their magnitude and direction, and identifying unbalanced forces.
  • #1
TyChi
8
0
1. Homework Statement

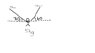
A 5kg monkey hangs initially at rest from two vines, A and B, as shown in the JPEG attached. Each of the vines is 10m long and has negligible mass.

a) Draw a force diagram labeling all forces acting on the monkey. (do not resolve the forces into components, indicate their directions though.)

b) What's the tention in vine B while the monkey is at rest?
 

Attachments

  • monkey.jpg
    monkey.jpg
    7.5 KB · Views: 1,050
Physics news on Phys.org
  • #2
It is a requirement that you please list what you believe may be relevant equations and that you show some attempt at a solution before we can give assistance. Thank you.
 

FAQ: Monkey force diagram and tension problem

1. What is a monkey force diagram?

A monkey force diagram is a visual representation of the forces acting on a monkey or an object that is being held by a monkey. It shows the direction and magnitude of the forces, as well as the objects or points where the forces are being applied.

2. How do you draw a monkey force diagram?

To draw a monkey force diagram, you first need to identify all the external forces acting on the monkey or the object being held by the monkey. Then, draw a dot to represent the monkey or object and draw arrows to represent the forces, with the length and direction of the arrows corresponding to the magnitude and direction of the forces. Finally, label each force and make sure to include a scale on the diagram.

3. What is tension in a monkey force diagram?

Tension is a force that is transmitted through a string, rope, or cable when it is pulled taut by two opposing forces. In a monkey force diagram, tension is represented by arrows that point away from the object being held by the monkey. The magnitude of the tension force is equal to the force being applied on the other end of the string or rope.

4. How do you calculate tension in a monkey force diagram?

To calculate tension in a monkey force diagram, you can use the formula T = mg + ma, where T is the tension force, m is the mass of the object being held, g is the acceleration due to gravity, and a is the acceleration of the object (if it is in motion). You can also use the Pythagorean theorem to calculate the magnitude of the tension force if the diagram is drawn to scale.

5. Why is it important to draw a monkey force diagram?

Drawing a monkey force diagram is important because it helps us visualize and understand the different forces acting on a monkey or an object being held by a monkey. It also allows us to accurately calculate the magnitude and direction of these forces, which is crucial in solving tension problems or predicting the motion of the object. Additionally, it helps us identify any unbalanced forces that may cause the monkey to lose its grip or the object to move in a certain direction.

Similar threads

Monkey accelerating up and down a rope
2
Replies
38
Views
3K
Potential Mistake in Free-Body Diagram
Replies
5
Views
1K
Correct vector diagram of forces
Replies
3
Views
1K
Find the magnitude of the electric force from 3 charges at vertices of a cube
Replies
17
Views
2K
Tension in a deformed cylindrical bag on a surface
Replies
18
Views
681
G-force diagram on a roller coaster?
Replies
5
Views
2K
Calculating Tension in Vines: A 5.0kg Monkey at Rest on Vines A and B
Replies
4
Views
3K
Solving Monkey Swing Physics Problem
Replies
4
Views
4K
Force Diagrams for Sliding Block on Inclined Plane
Replies
12
Views
3K
Find the tension in the two strings
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top