alexm
- 6
- 0
- Homework Statement
- Motion of rotating rig, find angle variation with control rod length
- Relevant Equations
- Trigonometry
Summary:: We have a rotating arm, offset from the centre of rotation by a certain length, which is controlled by varying the length of a control rod. Need the angle of the rotating arm in terms of length of the rod.
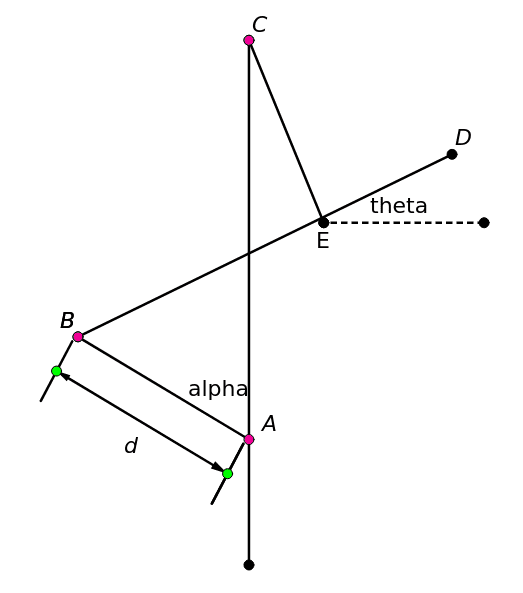
The blue line is a fixed column structure. CE and BD form the rotational arm, and AB is the control rod. The control rod and arm are free to rotate at the points shown (either end of the control rod, the join of the arm and the vertical column (AC)).
My question is, can anyone tell me the function that describes theta in terms of d (theta = f(d))? All lengths other than d are fixed and known. theta is the angle the rotational arm makes with the horizontal.
The pink joints show freedom of rotation.
Angle CED is fixed at 90 degrees.
Lengths LBE, LDE, LCE, LCA are also fixed.
When theta is 0, d = d0.
d = LAB and is variable.
[Moderator's note: Moved from a technical forum and thus no template.]
The blue line is a fixed column structure. CE and BD form the rotational arm, and AB is the control rod. The control rod and arm are free to rotate at the points shown (either end of the control rod, the join of the arm and the vertical column (AC)).
My question is, can anyone tell me the function that describes theta in terms of d (theta = f(d))? All lengths other than d are fixed and known. theta is the angle the rotational arm makes with the horizontal.
The pink joints show freedom of rotation.
Angle CED is fixed at 90 degrees.
Lengths LBE, LDE, LCE, LCA are also fixed.
When theta is 0, d = d0.
d = LAB and is variable.
[Moderator's note: Moved from a technical forum and thus no template.]
Last edited:
 !
!