Rotational Kinematics - Angle of a bar attached to a spinning rod

[bendezium]

Homework Statement

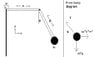
Problem statement: Please see the attached picture. A rigid rod rotates with constant angular velocity w. A rigid bar with length A is attached perpendicular to the rotating rod. A second rigid bar with length B is attached to the other end of bar A by a hinge. The hinge allows bar B to swing up and out, but not side to side (from a top view, bar A and bar B will be perfectly aligned). An object with mass m is attached to the far end of bar B. The angle of bar B with respect to the y-axis, theta, is unknown.

Known: length A, length B, angular velocity w, mass m

Assume: The rod and both bars are rigid; the object is a point mass; friction can be neglected;

Find: theta in terms of the known variables

Homework Equations

F = m * a
vt = w * r (angular velocity)
ar = w^2 * r (radial acceleration)

The Attempt at a Solution

Since w is constant, the system is not accelerating, so theta will be constant. My attached picture shows a free-body diagram of the mass. Its weight pulls it down, and centrifugal force pushes the mass outwards. The tension 'T' from bar B holds the mass in place. Here's what I've got:

Sum of all forces in the x direction = 0 = m * r * w^2 - T * sin(theta)
Sum of all forces in the y direction = 0 = T * cos(theta) - m * g

which implies

T * cos(theta) = m * g
T * sin(theta) = m * r * w^2

Here's where I'm stuck. Is r with respect to the point at the hinge, or the rotating rod? Which of the following is true:

r = B * sin(theta)
OR
r = B * sin(theta) + A

If I can get past this step, I can solve the problem. Thanks so much,

Eryk

EDIT: since the picture isn't approved yet, here it is on ImageShack: http://img189.imageshack.us/img189/4717/problemeqs.jpg

 

[RoyalCat]

What circle does the rotational motion of the mass draw? Around what axis does it rotate?
What does that tell you about how r should be measured?

 

[bendezium]

The mass draws a circle around the spinning rod, and not around the hinge. I believe that the length A should be taken into account, but my boss is trying to convince me that the length of A doesn't matter. Here's my choice:

r = B * sin(theta) + A

Could someone explain to me why I'm right or wrong? If I'm right, I need to be able to convince my boss that I am. We're electrical engineers working on a certain unnamed project, and it's been a while since we've taken these classes. His thoughts are that the hinge is also accelerating towards the center rod, and only the difference between the accelerations should be taken into account. I believe that the angle is dependent on the length A, and he believes the angle would be the same whether A was a millimeter or a kilometer.

Thanks,

Eryk

 

[RoyalCat]

Yes, that looks correct to me.
r=A+B\sin {\theta}
Geometrically, that is the distance of the mass from the axis of rotation, and the radius of the circular path it draws in its rotation.

Your boss is wrong. Relative acceleration is completely irrelevant here. And here's how I would convince him he's wrong:
The longer the rod A is, the further away from the axis of rotation, the mass would be.
The downwards force remains constant regardless of the distance from the axis of rotation.
In analysis of forces, you should consider the forces acting on the body and only the forces acting on the body, relative to certain frame of reference, anything else is irrelevant.

Looking at the mass from its own accelerated frame of reference, it is at equilibrium. Three forces act on it, the first is the force of gravity, the second is the force of the tension in the rod B and the third is the fictitious centrifugal force, pointing away from the axis of rotation:
\vec F_{D} =m\vec a_{r}

\vec a_r = \omega ^{2} r

A quick rundown of the forces reveals the following relations:
T\cos{\theta}=mg
T=\frac{mg}{\cos{\theta}}

T\sin{\theta}=m\omega ^{2} r
mg\tan{\theta}=m\omega ^{2} r
\tan{\theta}=\frac{\omega ^{2} r} {g}

And obviously, since your r is a purely geometric quantity, you can see that the angle does depend on the distance from the axis of rotation, and that includes depending on both the lengths A and B.

As a small exercise, you can substitute r with what you derived using A and B, and then draw your conclusions about Θ. :) It doesn't always exist.
EDIT:
Well, I tried doing that, but isolating Θ isn't that straightforward. I take back what I said, I think this problem might not be wholly analogous to what I cited below.

Consider this analogous problem:
A metal rod is rotating with constant angular velocity \omega
Attached to the rod is a string of negligible mass. Attached to the end of the string, is a mass m
What is the angle that the string is spread out at with respect to the rod?

In this problem, there is a bottom limit to how slow \omega can be. Go too slow, and the string won't spread out to create an angle Θ at all. Finding the critical \omega is an exercise in getting an equation that looks something like this:
\sin{\theta}=..., and then saying that since the right side of the equation is bound between ±1, then the left side must abide by the same limitation, and that gives you a limit on \omega

The answer in that case, does depend on the length of the string. The longer it is, the stronger the centrifugal force can be (It has higher upper cap, since the distance it can be from the axis of rotation is greater).

 

[bendezium]

Thank you RoyalCat,

I actually tried isolating theta before I even posted, and realized that it wasn't very easy to do. No big deal - that's what Maple is for.

I also thought of a second way to convince him. If you look at it from the rotating rod's perspective, it still has to provide a force of m * r * w^2 to keep bar A from flying away, with r = A + B * sin(theta). If bar A is still modeled as massless, since it's not moving, that force must be at the other end of bar A as well. That force must come from the mass on bar B.

Thanks again,
Eryk