DividedbyZero
- 11
- 0
Homework Statement
Problem:
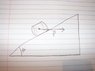
"On the 50 degree ramp below an empty barrel is sliding up it to get filled at a factory. The empty barrel has a mass of 24kg and has an initial velocity of 1.2m/s. The kinetic coefficient of friction between the barrel and the ramp is μ =0.48 Finally a horizontal force is acting on the barrel of 320N.
1.)What is the barrel's acceleration?
2.)What is the direction of the barrel's acceleration?
3.) How far up the ramp does the barrel go before its velocity is zero?"
First picture is of what is given
Homework Equations
F=ma (of course)
accelerations will involve x or y components with regard to theta (sin(σ) and cos(σ))
?Kinetic formulas? Δx=
The Attempt at a Solution
Second picture attachment is a picture of my diagram so far. Is it missing a force going down the ramp? Parallel to the friction force?
A.)Not sure where to start here.
B.) The acceleration is down the ramp because it is slowing to a stop. Correct?
C.) Solvable after I find acceleration in part A? Using Δx= Vi(t)+ 0.5(a)t^2 where Vi is initial velocity. Or on second thought perhaps this one if you can not find time: V^2=Vi^2 + 2a(xΔx)
Please and thank you!